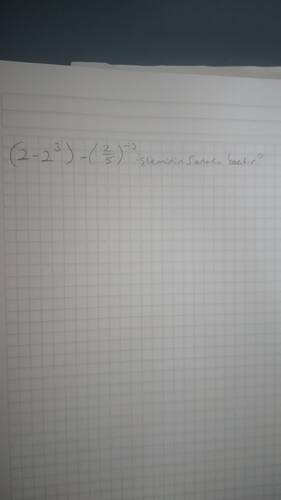What is the solution to the expression ((2 - 2^3) - \left(\frac{2}{5}\right)^{-3} )?
Answer:
To solve the expression ((2 - 2^3) - \left(\frac{2}{5}\right)^{-3}), we will break it down step by step.
Step 1: Simplify (2 - 2^3)
[ 2^3 = 8 ]
So, (2 - 2^3 = 2 - 8 = -6).
Step 2: Simplify (\left(\frac{2}{5}\right)^{-3})
A negative exponent means we take the reciprocal of the base and then raise it to the positive of that exponent.
[
\left(\frac{2}{5}\right)^{-3} = \left(\frac{5}{2}\right)^3
]
Now calculate (\left(\frac{5}{2}\right)^3):
[
\left(\frac{5}{2}\right)^3 = \frac{5^3}{2^3} = \frac{125}{8}
]
Step 3: Combine Both Parts
Now, we need to subtract the result of (\left(\frac{2}{5}\right)^{-3}) from ((2 - 2^3)):
[
-6 - \frac{125}{8}
]
To subtract these values, we rewrite (-6) as (-\frac{48}{8}):
[
-\frac{48}{8} - \frac{125}{8} = -\frac{48 + 125}{8} = -\frac{173}{8}
]
Final Answer:
The solution to the expression ((2 - 2^3) - \left(\frac{2}{5}\right)^{-3}) is (-\frac{173}{8}).