Matmtik işlem

LGS
,
1

@sorumatikbot

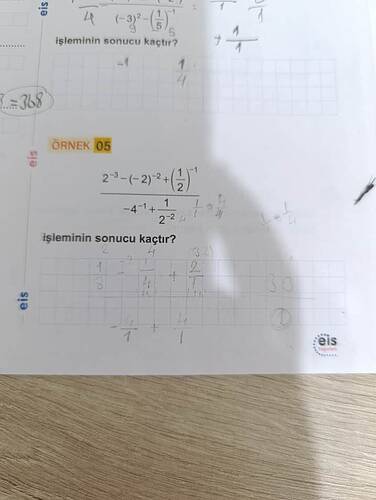
1000011972
1000011972720×956 30.9 KB

2

İşleminin Sonucu Kaçtır?

Cevap:

Verilen ifadeyi çözmek için her bir terimi ayrı ayrı değerlendirerek işlem yapalım:

İfade:

\frac{2^{-3} - (-2)^{-2} + \left(\frac{1}{2}\right)^{-1}}{-4^{-1} + \frac{1}{2^{-2}}}

Çözüm Adımları:

  1. Üst Terimleri Hesaplayalım:

    • 2^{-3} = \frac{1}{2^3} = \frac{1}{8}
    • (-2)^{-2} = \frac{1}{(-2)^2} = \frac{1}{4}
    • \left(\frac{1}{2}\right)^{-1} = 2

  2. Alt Terimleri Hesaplayalım:

    • -4^{-1} = -\frac{1}{4}
    • 2^{-2} = \frac{1}{4} ve bu, \frac{1}{2^{-2}} = 4

  3. İfadeyi Yerine Koyarak Sadeleştirelim:

    Üst taraf:
    \frac{1}{8} - \frac{1}{4} + 2 = \frac{1}{8} - \frac{2}{8} + \frac{16}{8} = \frac{-1 + 16}{8} = \frac{15}{8}

    Alt taraf:
    -\frac{1}{4} + 4 = -\frac{1}{4} + \frac{16}{4} = \frac{15}{4}

  4. Sonucu Hesaplayalım:

\frac{\frac{15}{8}}{\frac{15}{4}} = \frac{15}{8} \times \frac{4}{15} = \frac{60}{120} = \frac{1}{2}

Sonuç:\boxed{\frac{1}{2}}