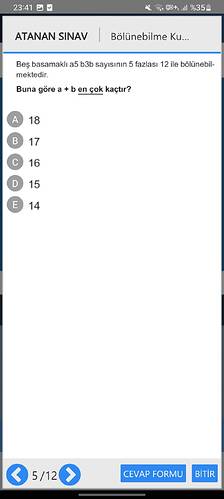
Beş basamaklı a5b3b sayısının 5 fazlası 12 ile bölünebilmektedir. Buna göre a + b en çok kaçtır?
Bu sorunun çözümünü adım adım inceleyelim:
-
Verilen Sayı Üzerinde Çalışma:
- Sayı: a5b3b
- Bu sayı, 10a + 50 + b \cdot 10 + 3 + b = 10000a + 5000 + 100b + 30 + b şeklinde gösterilebilir ve sayının 5 fazlası, 10000a + 5000 + 101b + 35 olacaktır.
-
12 ile Bölünebilme Koşulu:
- Sayının 5 fazlası 12 ile bölünmelidir yani: 10000a + 5085 + 101b \equiv 0 \pmod{12} olmalıdır.
-
Sayıları Sadeleştirme:
- 10000 mod 12 = 4 olduğuna, 5085 mod 12 = 9 olduğuna göre: 4a + 101b + 9 \equiv 0 \pmod{12}
- 101 sayısı 12’ye bölündüğünde 5 kalanını verir; dolayısıyla: 4a + 5b + 9 \equiv 0 \pmod{12}
-
Denklemleri Çözme:
- 4a + 5b + 9 \equiv 0 \pmod{12} den gelişi güzel değerler deneyelim.
- 4a + 5b \equiv 3 \pmod{12} olur.
-
a ve b’nin Maksimum Toplamının Bulunması:
- a’yı ve b’yi deneme yanılma yaparak inceleyelim. b’nin alabileceği en yüksek değer 9’dur.
- 4a + 5 \times 9 = 3 (mod 12)
- Bunu çözdüğümüzde: 4a + 45 \equiv 3 (mod 12) → 4a \equiv -42 (mod 12) → 4a \equiv 6 (mod 12) olur.
- En yüksek a değeri 9 olabilir, bu olduğunda: 4 \times 9 = 36 (mod 12) → 36 \equiv 0
- Bu uygun değil, a’yı düşürüp 6 denediğimizde: 4 \times 6 = 24 ve bu mod 12 için uygundur.
Sonuçta, a = 6, b = 9 ile a + b = 15 olur. Cevap: D) 15tir.