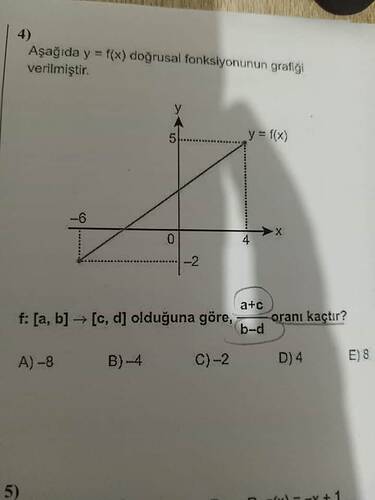
Aşağıda y = f(x) doğrusal fonksiyonunun grafiği verilmiştir. f: [a, b] → [c, d] olduğuna göre, (a+c)/(b-d) oranı kaçtır?
Çözüm:
Doğrusal bir fonksiyonun grafiği genellikle şu formattadır:
[
y = mx + n
]
burada ( m ) eğimi, ( n ) ise y-eksenini kestiği noktayı temsil eder.
Adım 1: Eğim (m) ve Y-ekseni Kesim Noktasını (n) Belirleme
-
Grafikte, x ekseni -6’dan 4’e kadar, y ekseni ise -2’den 5’e kadar uzanıyor.
-
Eğim ( m ) şu şekilde bulunabilir:
[
m = \frac{\text{y-değişim}}{\text{x-değişim}} = \frac{5 - (-2)}{4 - (-6)} = \frac{7}{10}
] -
Grafikte ( n = 0 ) gözüküyor. Yani grafiğin sıfırdan geçtiğine göre, y-eksenini 0’dan kesiyor.
-
Doğru denklemi ( y = \frac{7}{10}x + 0 ), yani ( y = \frac{7}{10}x ) oldu.
Adım 2: Fonksiyonun Uç Değerlerini Bulma
Verilen f: [a, b] → [c, d] fonksiyonu için, b-d aralığı, x ekseninde ([-6, 4]) ve y ekseninde ([-2, 5]) olarak verilmiştir.
- ( a = -6 ) ve ( b = 4 )
- ( c = -2 ) ve ( d = 5 )
Adım 3: Oranı Hesaplama
- (a+c) = (-6 + (-2) = -8)
- (b-d) = (4 - 5 = -1)
Oran:
[
\frac{a+c}{b-d} = \frac{-8}{-1} = 8
]
Sonuç:
Final Cevap:
Bu koşullar altında, (a+c)/(b-d) oranı 8’dir. Bu nedenle cevap E) 8.