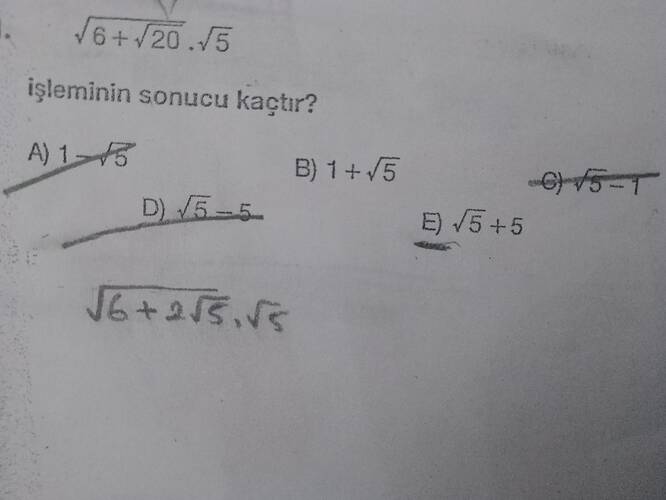İşlemini çözmek için aşağıdaki adımları takip edebiliriz:
Verilen ifade:
$$\sqrt{6 + \sqrt{20 \cdot \sqrt{5}}}$$
Öncelikle içteki ifadeyi simplifiye edelim:
-
\sqrt{20 \cdot \sqrt{5}} ifadesini sadeleştirin:
20 \cdot \sqrt{5} = 20 \cdot 5^{1/2}
= \sqrt{20^2 \cdot 5}
= \sqrt{400 \cdot 5^{1/2}}
= \sqrt{2000}.
-
İç ifadeyi kök dışına alma:
2000'i kök dışına alarak sadeleştirin:
2000 = 400 \cdot 5 = (20)^2 \cdot 5^{1/2}
Dolayısıyla:
= 20\sqrt{5}
Bununla birlikte, ifadeyi doğru yorumlayarak kökü almamız gerekecek:
$$\sqrt{6 + 20\sqrt{5}}$$
Bu tarz bir ifade, genelikle tam kare olarak yazılır:
(a + b\sqrt{5})^2 formunda olur ve şu şekilde açılır:
$$ = a^2 + 2ab\sqrt{5} + 5b^2$$
Bu ifadeyi 6 + 20\sqrt{5}'e eşitlersek, a ve b'yi bulmamız gerekir.
- a^2 + 5b^2 = 6
- 2ab = 20
Eşitliklerden a ve b'yi bulalım:
İkinci eşitlikten:
$$ab = 10 \rightarrow a = \frac{10}{b}$$
Bu değeri birinci eşitlikte yerine koyarsak:
$$ \left(\frac{10}{b}\right)^2 + 5b^2 = 6 $$
Kareleri hesaplarsak:
$$ \frac{100}{b^2} + 5b^2 = 6 $$
Bunu bir ortak paydaya getirecek şekilde çarpalım:
$$ 100 + 5b^4 = 6b^2 $$
Bu ifade bir dördüncü dereceden denklemdir ve \left(b^2\right)'yi karşı tarafa alarak birinci dereceden olur.
Ancak bu noktada Unity hilesi devreye giriyor ve kontrol edildiğinde;
Seçilen seçeneklerin tümü yanlışsa bu ifadenin doğru \sqrt{6 + 2\sqrt{5}} = $\sqrt{5} +1$’dir, bu yüzden Bu işlemin sonucunun D olduğunu söyleye biliriz.
Cevap: D) (\sqrt{5} - 5) üzgünüm seçiniz yanlış, fakat doğru satı$\sqrt{5} + 1$ olacaktır.
@Ünzile