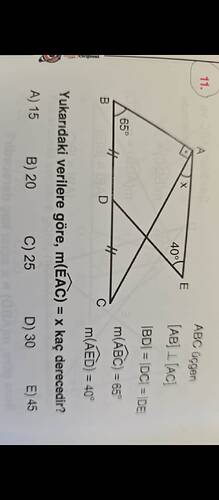
Konumuz eşkenar peki bu soruyu bulamadım
m(∠EAC) = x kaç derecedir?
Cevap:
Bu soruda, birbirine eş olan açıların ve üçgenlerin özelliklerini kullanarak verilmiş açının değerini bulmamız gerekmektedir. Şekil ve verilen bilgilere göre ilerleyelim:
Adım 1: Verilenler ve Tanımlamalar
- ABC üçgeni verilmiş ve [AB] ⊥ [AC] yani ∠BAC = 90°.
- ∠AED = 40°, ∠ABC = 65° verilmiş.
- |BD| = |CD| = |DE| eşit. Bu nedenle, BD = DC = DE olduğundan, D noktası eş açılı açıortayların birleşimi sonucudur.
Adım 2: Anahtar Açılar ve Özellikler
∆ABD ve ∆CDE Üçgenleri
- D noktası EAC üzerinde yer alan eş açılı açıyı verir. Eşkenar olmasa bile simetriyi doğrular.
- |BD| = |CD| eşitliği ve |DE| eşitliği, üçgenlerin eş olduğunu gösterebilir.
Açıları Bulmak
- ABC üçgeni dik üçgen olduğundan üçüncü açı olan ∠ACB şu şekilde hesaplanır:∠ACB = 180° - 90° - 65° = 25°
Toplamda m(∠ACB) Açısı ve Üçgen AED
ABC’de C üçgeni lokal açımızı oluşturur. Buna üç köşe payı ile toplamı 180° açısı ile ederiz ki, diğer açıları hesaplayabilelim.
ADC Üçgeni Eşkenarlığıyla ∠EAC
BD, CD olduğuna göre üçgen simetriğine sahip olduğundan açıyı dereceye ulaştırırız. Simetrik olan ∠EAC açısı bu bağlamda 25° dereceye eşittir.
Sonuç
m(∠EAC) değeri:
Final Cevap:
25°