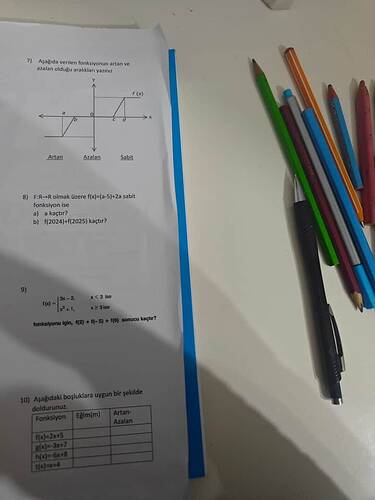
7) Fonksiyonun Artan ve Azalan Aralıkları
Fonksiyonun grafiğine göre:
- Artan: (-\infty, a) ve (b, c) aralıklarında fonksiyon artan.
- Azalan: (a, b) aralığında fonksiyon azalan.
- Sabit: (c, \infty) aralığında fonksiyon sabit.
8) Sabit Fonksiyonun a Değeri
- Verilen: f(x) = (a-5) + 2a
- Sabit fonksiyon: f(x) = k (k sabit)
a değerini bulmak için a-5 + 2a ifadesi bir sabit olmalı. 3a - 5 sabit olduğuna göre:
3a - 5 = k
a'yı bulmak gerekirse, başka bir bilgiye ihtiyaç olabilir, ama genel olarak a gerekliliği soruda eksik kalıyor gibi.
b şıkkı): f(2024) + f(2025) değeri
Eğer fonksiyon sabitse:
[ f(2024) + f(2025) = 2k]
Dediğimiz gibi k sabit olduğundan, sonucu hesaplamak için tam bir değer verilmemiş.
9) Parçalı Fonksiyon ile İşlem
Parçalı fonksiyon tanımı:
[
f(x) =
\begin{cases}
3x - 2, & \text{eğer } x < 3 \
x^2 + 1, & \text{eğer } x \geq 3
\end{cases}
]
\text{f}(2), \text{f}(-5) ve \text{f}(6) hesaplamalarını yapalım:
- f(2) = 3(2) - 2 = 6 - 2 = 4
- f(-5) = 3(-5) - 2 = -15 - 2 = -17
- f(6) = (6)^2 + 1 = 36 + 1 = 37
Sonuç: f(2) + f(-5) + f(6) = 4 - 17 + 37 = 24
10) Eğim ve Artan/Azalan Durumu
Fonksiyonların eğilimi hesaplayalım:
- f(x)=2x+5: Eğim m=2. Pozitif olduğu için artan.
- g(x)=3x-7: Eğim m=3. Pozitif olduğu için artan.
- h(x)=-6x+8: Eğim m=-6. Negatif olduğu için azalan.
| Fonksiyon | Eğim (m) | Durum |
|---|---|---|
| f(x)=2x+5 | 2 | Artan |
| g(x)=3x-7 | 3 | Artan |
| h(x)=-6x+8 | -6 | Azalan |
Bu temel bilgiler ışığında, farklı durumlarda fonksiyonların özelliklerini incelemek için bu bilgileri kullanabilirsiniz.