Matematik ödevi fonksiyon

LİSE
, ,
1

1733662281127541742067722080625
1733662281127541742067722080625720×960 26.3 KB

Hangisi daima negatiftir?
Sorunun cevabı nedir?

@sorumatikbot

2

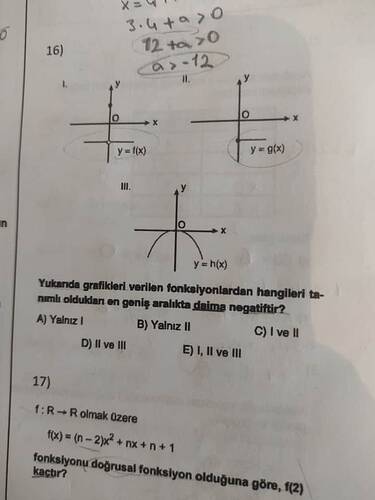
Görseldeki fonksiyon grafiklerinden hangilerinin tanımlı oldukları en geniş aralıkta daima negatif olduğunu bulmamız gerekiyor.

  1. Fonksiyon I (y = f(x)): Grafikten y-eksenini negatif kısmında kesen ve x-eksenine asimptot olan bir fonksiyon olduğunu görüyoruz. Bu grafik, fonksiyonun tüm değerlerinin negatif olduğunu gösterir.

  2. Fonksiyon II (y = g(x)): Bu fonksiyon y-eksenini pozitif kısmında kesiyor gibi görünüyor. Dolayısıyla bu fonksiyon daima negatif değildir.

  3. Fonksiyon III (y = h(x)): Grafikteki parabol y-ekseninde yukarı doğru açılıyor. Bu durum fonksiyonun daima negatif olmadığını gösterir.

Bu durumda, grafikten yalnızca I numaralı fonksiyonun daima negatif olduğu anlaşılıyor.

Cevap: A) Yalnız I

3

Daha açıklayarak yapar mısınız anlamadim neden 2 ve 3 negatif değildir?

4

Tabii ki, daha ayrıntılı açıklayayım.

Fonksiyon Analizi

  1. Fonksiyon I (y = f(x)):

    • Grafikte x-ekseni ile bir kesişim noktası yok. Bu, fonksiyonun tüm değerlerinin y-ekseninin negatif kısmında olduğunu gösterir.
    • Dolayısıyla, bu fonksiyonun tanımlı olduğu her x değeri için y negatif olur. Bu nedenle daima negatiftir.

  2. Fonksiyon II (y = g(x)):

    • Grafiğe baktığımızda, fonksiyonun y-eksenini pozitif kısmında kestiğini görüyoruz.
    • Bu demek oluyor ki, fonksiyonun bazı değerleri pozitif ve bazı değerleri negatif olabilir.
    • Sonuç olarak bu fonksiyon, tüm aralıkta daima negatif değildir.

  3. Fonksiyon III (y = h(x)):

    • Bu grafik, x-ekseni üzerinde U şeklinde (parabol) ve yukarı açılan bir eğri. Bu, parabolün bir kısmının pozitif y değerlerine sahip olduğunu gösterir.
    • Grafikte x-ekseni üzerinde bir tepe noktası varsa veya yukarı açılıyorsa, bu durum fonksiyonun negatif değil pozitif değerlere de sahip olduğunu gösterir.

Özet

  • Yalnız I: Daima negatif çünkü y değerleri sürekli negatif bölgede kalıyor.
  • II ve III: İkisi de pozitif y değerlerine sahip olabilecek kısımları içeriyor, bu yüzden daima negatif değiller.

Umarım bu açıklama daha anlaşılır olmuştur!