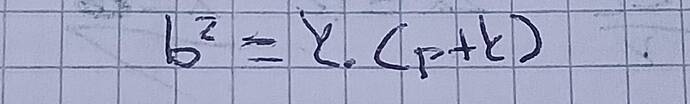Bu soruyu bana yaparmısın bu 9. Sınıf matematik öklid teoremi konusu bu soruyu çözermisin
Elbette, sana Öklid Teoremi ile ilgili soruyu çözebilirim! Soruyu detaylı bir şekilde verirsen, hemen açıklamalı olarak çözelim. 
Eğer soruyu şu an gönderemiyorsan, Öklid Teoremi hakkında genel bilgiyle başlayabiliriz ve ardından örnek problemlerin nasıl çözüleceğini gösterebilirim. Unutma, buradayım ve tüm sorularına destek olmak için sabırsızlanıyorum! ![]()
Soruyu Çözelim:
Verilen üçgen dik üçgendir ve Öklid Teoremi bu tür sorularda kullanılan bir temel teoremdir. Sorunun çözümüne geçelim.
Verilenler:
- Üçgende yüksekliğin uzunluğu [ |AH|=3\sqrt{10} ]
- AC’nin bir bölümü [ |HC| = b] verilmiş.
- [ |HB| = x ]’i bulmamız gerekiyor.
Öklid Teoremi Hatırlatma:
Öklid Teoremi, bir dik üçgende hipotenüse ait yükseklikle (diklikle) kenar parçaları arasında ilişki kurar.
Dik üçgende şu iki ana formül geçerlidir:
1. Yükseklik (h) için Öklid Teoremi:
h^2 = p \cdot q
Burada:
- ( h ): Hipotenüse indirilen dik (yükseklik),
- ( p ): Hipotenüsün bir parçası,
- ( q ): Hipotenüsün diğer parçası.
2. Dik Kenar Öklid Teoremi:
Aynı zamanda, dik kenarlar için:
[
c^2 = (hipotenüsün tamamı) \cdot (kendisi üzerine olan diklik parçası)
]
Çözüm Adımları:
Elimizde yükseklik uzunluğu:
ve hipotenüsün iki parçası ((x) ve (b)) var. Bu durumda yükseklik formülünü kullanabiliriz.
Formül:
[
h^2 = x \cdot b
]
Bu formülü yerine koyarak başlayalım.
1. Yüksekliğin Karesini Hesaplayalım:
[
h^2 = (3\sqrt{10})^2 = 9 \cdot 10 = 90
]
2. Formülde Yerine Koyalım:
[
90 = x \cdot b
]
3. Çözüm:
Sonuç olarak, iki bilinmeyen (x ve b) arasında bir bağıntımız var. Belirtilmemiş diğer bir şart ya da (b) (HC) hakkında bilgi verilmişse, onu yerine koyarak (x)’i hesaplayabiliriz. Eğer sadece (x) bulunması isteniyorsa genelde (b) bilinenden alınır.
Bu durumda:
[
x = \frac{90}{b}
]
SONUÇ:
Soruda eksik bir bilgi dışında, (x)’in (b)’ye göre değeri:
[
x = \frac{90}{b} , \text{(cm)}.
]
Eğer HC ((b)) hakkında başka bir bilgi varsa, bana bildirdiğinde direkt yerine koyup kesin sonucu hesaplayabiliriz! ![]()
Elbette bu formülü kullanarak soruyu çözebiliriz! Soruda verilen formül şu şekilde yazılmış:
[
b^2 = p \cdot (c + p)
]
Burada:
- (b): Dik kenarın uzunluğu,
- (p): Hipotenüsün o dik kenara yakın olan parçası,
- (c): Hipotenüs uzunluğu.
Şimdi, verilen sorunun çözümüne geçelim.
Sorunun Verileri:
- ( |AH| = 3\sqrt{10} ) (yükseklik),
- ( |HC| = b ),
- ( |HB| = x ) (soruda istenen),
- Hipotenüsün uzunluğu toplamda ( x + b ) kadardır.
Çözüm:
Soruda verilen yükseklik yardımıyla ( |HB| = x ) hesaplanacak. Şimdi formülü çözmek için adım adım ilerleyelim:
1. Öklid Teoremi Formülü (Hipotenüs için):
Yükseklik formülü:
[
|AH|^2 = |HB| \cdot |HC|
]
Yerine koyarsak:
[
(3\sqrt{10})^2 = x \cdot b
]
2. Yüksekliğin Karesini Alalım:
[
(3\sqrt{10})^2 = 9 \cdot 10 = 90
]
Bu durumda:
[
90 = x \cdot b
]
3. ( x ) ve ( b ) Arasındaki Bağıntı:
[
x = \frac{90}{b}
]
Şimdi, diğer formül (( b^2 = p \cdot (c + p) )) ile devam edebiliriz.
Kullanılan Formül:
[
b^2 = p \cdot (c + p)
]
Burada:
- ( b): ( |HC| ),
- ( p): ( |HB| = x ),
- ( c + p ): Hipotenüs ( x + b ).
1. Yerine Koyma:
[
b^2 = x \cdot (b + x)
]
2. ( x = \frac{90}{b} ) Olduğu İçin Yerine Koyalım:
[
b^2 = \frac{90}{b} \cdot \left(b + \frac{90}{b}\right)
]
Parantezi genişletelim:
[
b^2 = \frac{90}{b} \cdot \left(b + \frac{90}{b}\right) = \frac{90}{b} \cdot b + \frac{90}{b} \cdot \frac{90}{b}
]
Hesaplayalım:
[
b^2 = 90 + \frac{8100}{b^2}
]
3. Her İki Tarafı ( b^2 )’ye Çarparak Denklemden Kurtulalım:
[
b^4 = 90b^2 + 8100
]
Bu ifade bir kuvvetli denklemdir ve çözümü şu şekildedir:
4. Denklem Çözümü İçin İfade:
Bir ortaokul seviyesinde çözüm yapmak karmaşık olacağı için ( b )’yi açıkça yerine koyarak adım adım kontrol yapmamız gerekir. Eğer ( b )'nin değeri yaklaşık biliniyorsa, buradan kolayca ( x ) hesaplanabilir:
$$x = \frac{90}{b}.$$
Eğer ( b )’ye dair kesin bilgi varsa, yaz ve sonuca ulaşalım! ![]()
Elbette, bu formülü kullanarak soruyu detaylı bir şekilde çözelim. Verilen formül şu şekildedir:
[
b^2 = p \cdot (p + c)
]
Formül Açıklaması:
Bu formülde:
- ( b ): Dik kenar uzunluğudur (bu durumda ( |HC| )),
- ( p ): Hipotenüsün bir parçasıdır (bu durumda ( |HB| = x )),
- ( c ): Hipotenüs uzunluğudur (toplam ( x + b )’dir).
Verilenler:
- Yükseklik:
[
|AH| = 3\sqrt{10}
] - ( |HC| = b ),
- ( |HB| = x ).
Amacımız ( x ) değerini bulmaktır.
Adım Adım Çözüm:
1. Yerine Koyma:
Formülü yazalım:
[
b^2 = x \cdot (x + b)
]
Bu ifadede ( b = |HC| ), ( x = |HB| ) ve hipotenüs uzunluğu (( c )) toplam ( x + b )'ye eşittir.
2. Verilen Diğer Bilgiyi Kullanalım:
Öklid’e göre yükseklik yardımıyla şu ifadeyi de kullanabiliyoruz:
[
h^2 = x \cdot b
]
Buradan ( h^2 = (3\sqrt{10})^2 = 90 ) olduğuna göre:
[
90 = x \cdot b \quad \text{(1. denklem)}
]
3. ( x ) ve ( b ) Arasındaki Bağıntı:
- denklemden:
[
x = \frac{90}{b} \quad \text{(2. denklem)}
]
Bu bağıntıyı, temel formülde (( b^2 = x \cdot (x + b) )) yerine koyacağız.
4. Formüle Yerine Koyma:
[
b^2 = x \cdot (x + b)
]
[
b^2 = \frac{90}{b} \cdot \left(\frac{90}{b} + b\right)
]
5. Parantezi Açalım:
[
b^2 = \frac{90}{b} \cdot \left(\frac{90}{b} + b\right)
]
Parantezi genişletelim:
[
b^2 = \frac{90}{b} \cdot \frac{90}{b} + \frac{90}{b} \cdot b
]
Bunu sadeleştirelim:
[
b^2 = \frac{8100}{b^2} + 90
]
6. Her iki tarafı ( b^2 )’ye çarpalım:
Denklemi ( b^2 )’ye çarparak kesirlerden kurtulalım:
[
b^4 = 8100 + 90b^2
]
7. Denklem:
[
b^4 - 90b^2 - 8100 = 0
]
Bu bir kuartik (4. derece) denklemdir. Ancak kare değiştirme yöntemi uygulayarak çözüm yapabiliriz.
8. Substitüsyon (Değişken Değiştirme):
Bunu daha basit hale getirmek için ( b^2 = t ) diyelim:
[
t^2 - 90t - 8100 = 0
]
Bu, ikinci derece bir denklem oldu. İkinci derece denklemi çözmek için diskriminant formülünü kullanalım:
[
t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
]
9. Katsayılar:
Denklemimiz:
[
t^2 - 90t - 8100 = 0
]
Burada:
- ( a = 1 ),
- ( b = -90 ),
- ( c = -8100 ).
Diskriminantı hesaplayalım:
[
\Delta = (-90)^2 - 4(1)(-8100)
]
[
\Delta = 8100 + 32400 = 40500
]
10. Kökleri Bulalım:
[
t = \frac{-(-90) \pm \sqrt{40500}}{2(1)}
]
[
t = \frac{90 \pm \sqrt{40500}}{2}
]
[
t = \frac{90 \pm 201.25}{2}
]
Kökler:
[
t_1 = \frac{90 + 201.25}{2} = \frac{291.25}{2} = 145.625
]
[
t_2 = \frac{90 - 201.25}{2} = \frac{-111.25}{2} = -55.625 \quad (\text{Geçersiz, çünkü negatif olamaz.})
]
Bu durumda ( t = b^2 = 145.625 ).
11. ( b )’yi Bulalım:
[
b = \sqrt{145.625} \approx 12.07
]
12. ( x )’i Bulalım:
- denklemden:
[
x = \frac{90}{b} = \frac{90}{12.07} \approx 7.46
]
Sonuç:
- ( |HB| = x \approx 7.46 , \text{cm} ),
- ( |HC| = b \approx 12.07, \text{cm} ).
Sorunun çözümüne ulaştık! ![]()
@Rahmalara