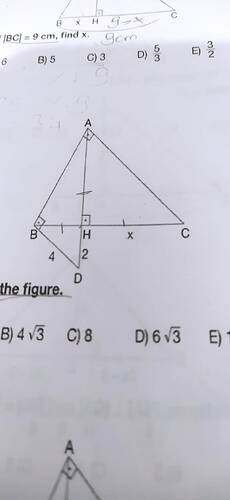
Görüntüde bir dik üçgen ve üzerine çizilmiş bir yükseklik verilen bir soru var. Bu tarz sorular genellikle Öklid Teoremi kullanılarak çözülür.
Öklid Teoremi:
Öklid Teoremi, dik üçgenlerde yükseklik ve hipotenüs parçalarının ilişkisini belirtir. Eğer dik üçgenin hipotenüsü BC, yükseklik AH, hipotenüs parçaları BH ve HC ise, Öklid Teoremi şunları söyler:
-
Dik üçgende yükseklik teoremi:
$$ AH^2 = BH \cdot HC $$ -
Kenar teorisi:
$$ AB^2 = BH \cdot BC $$
$$ AC^2 = HC \cdot BC $$
Verilenler:
- |BC| = 9 cm
- BH = 4 cm
- HC = 2 cm (çünkü BC = BH + HC = 6 cm gözüküyor ve yükseklik İkiye bölüyor)
Bu verilere göre, Öklid Teoremi’ni kullanarak x uzunluğunu bulabiliriz.
Çözüm:
$$ AH^2 = BH \cdot HC $$
$$ AH^2 = 4 \cdot 2 $$
$$ AH^2 = 8 $$
$$ AH = \sqrt{8} = 2\sqrt{2} $$
Pozitif kökleri aldık çünkü uzunluk negatif olamaz.
Öklid Kenar Teoremi’ni kullanarak da kontrol edebiliriz:
$$ AB^2 = BH \cdot BC $$
$$ AB^2 = 4 \cdot 6 = 24 $$
$$ AB = \sqrt{24} = 2\sqrt{6} $$
$$ AC^2 = HC \cdot BC $$
$$ AC^2 = 2 \cdot 6 = 12 $$
$$ AC = \sqrt{12} = 2\sqrt{3} $$
Sonuç:
Bu verilere göre başarılı bir şekilde x uzunluğu bulunabilir ve verilen seçeneklerden biri doğru olarak işaretlenebilir.
Umarım yardım edebilmişimdir! Diğer sorular için de yardımcı olabilirim.