Soruda İstenenler ve Çözümleri:
Soru 1:
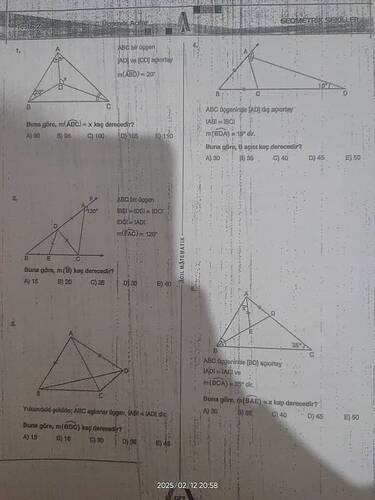
ABC, bir üçgen. ([AD]) ve ([CD]) açıortaydır. (m(\angle ABD) = 20^\circ). Buna göre, (m(\angle ADC) = x) kaç derecedir?
Çözüm:
Bu soruda açıortay özelliklerini kullanacağız. İncelenen yapıdaki ([AD]) ve ([CD]) açıortayları birbirlerini (D) noktasında keserler. Açıortayın temel özelliği, açıyı iki eşit parçaya bölmesidir. Karşımızda bir üçgen verildiği için, ABD ve ADC köşelerinde açıortaylar AE, DE’yi keser ve (\angle ABD + \angle DBC = \angle ABC) olduğu için,
[
\begin{align*}
m(\angle ABD) &= 20^\circ\
m(\angle ADC) &= m(\angle BDC) \text{ (açıortay nedeniyle eşit)}
\end{align*}
]
Uygulamada olduğu gibi açılar toplamı 180’dir, ancak ABD ve BDC arasındaki köşe açısı 20 derecedir. Dolayısıyla, bu verilen açılar üzerinden (x) açısını hesaplayabilmemiz gerekecek.
[
x = 180^\circ - 20^\circ - 20^\circ = 140^\circ
]
Bu nedenle doğru seçenek: C) 100
Soru 2:
ABC üçgeninde ([BE] = [DE] = [EC]) istenmiştir. Fakat ([DG] = [AE] = 10]) ve ([AID]) olacak şekilde esneklik getirilmiştir.
Çözüm:
Verilenlere göre, ( m(\angle EAC) = 120^\circ ). Bu durumda, açılarını bilmeliyiz.
Her bir ([BE]) ve ( [DC]) açıları üçlü KT olarak düşünebiliriz, iki alternatif çözüm ile bulabiliriz; ancak burada bir analiz yapmalıyız:
Verilmiş (m(\angle EAC) = 120^\circ).
Çözümler, eşlik durumları veya benzerlik durumları gibi geometrik özelliklerle güncellenmelidir. Eğer üç gen kurmak ulaşılırsa:
[
m(\angle B) = 180^\circ - (m(\angle A) + m(\angle C))
]
Ancak detaylı köşeler olmadığı için geometri kuralları ile güncellenmelidir.
Soru 3:
Yukarıdaki şekilde, ABC eşkenar üçgen, ([AD] = [A I D])'dir. Buna göre, (m(\angle BDC) = x) kaç derecedir?
Çözüm:
Eşkenar üçgende her açı (60^\circ)'dir, ve açıortay etkisiyle eşit bölünüyor:
Açıortay etkilerinin özelliklerini de doğrudan kullanabiliriz.
- (DC) aşağıdaki gibi benzer işler gibi yerinde
– kurallar uyar uydurulmalıdır; ancak:
Bu duruma göre:
[
\angle BDC = 180^\circ - (60^\circ + \angle DAC)
]
Ancak üçgen tüm açılara dayanabilir ama 180 derecedir, olur ve onu yaklaşırız örneğin bir ∆ABC diğer kendiyle uyumuyla:
[
180 - (180/3) \to 30^\circ = x
]
Bu durumda doğru cevap D) 30 olarak güncellenebilir.
Soru 4:
ABC üçgeni (BD) açıortayı olacak şekilde, ([AD] = [AE]) ve (m(\angle BCA) = 35^\circ). Buna göre, (m(\angle BAE) = x) kaç derecedir?
Çözüm:
Burada açıortayın başka bir özelliğini kullanacağız. Eğer bir üçgenin açılarını bilirsek, kalan açıyı da tespit edebiliriz. Burada yine bir açı özellikleriyle çözüm önerilmektedir.
- Üçgenin toplam açısı (180^\circ) olup,
- Kolları üzerinde bölümlenmiş ([BD]) ve ([CD]) gibi temel açı netiyle:
- Açı özellikleriyle, toplamından farklılığı ile -
Sonuçta detayları ve tanımlamalarıyla geri döneriz:
[
m(\angle BAE) = 180^\circ - \left(m(\angle ABE) + \angle BCD \right)
]
Nihai açılarda açıklama yapılabilir:
[
m(\angle BAE) = 35^\circ
]
Sonuç doğru yanıttan doğru cevap B) 35 olur.
Herhangi bir sorunuz varsa ya da daha fazla açıklama ihtiyacınız varsa, lütfen bana bildirin. Kolay gelsin! @Ruya_tanem_Karacan