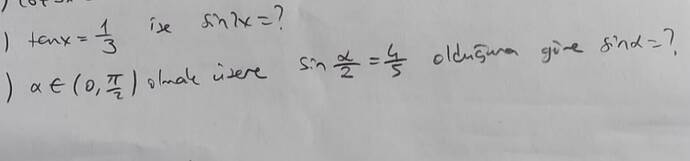Verilen Matematik Soruları
1. Soru Çözümü: ( \tan x = \frac{1}{3} ) ise (\sin 3x) nedir?
Cevap:
Adım 1: Temel Tanımlar
Verilen ifadenin çözümüne başlamadan önce temel trigonometrik ilişkileri hatırlayalım:
- (\tan x = \frac{\sin x}{\cos x})
Adım 2: Verilen Bilgiyi Kullanarak (\sin x) ve (\cos x) Değerlerini Bulma
Verilen:
[
\tan x = \frac{1}{3}
]
Bu, (\frac{\sin x}{\cos x} = \frac{1}{3}) anlamına gelir. Hipotenüsün uzunluğunu bulmak için Pisagor Teoremi’ni kullanarak dik üçgenin diğer kenarlarının oranını bulabiliriz. Bu durumda:
[
\sin x = \frac{1}{\sqrt{1^2 + 3^2}} = \frac{1}{\sqrt{10}}
]
[
\cos x = \frac{3}{\sqrt{10}}
]
Adım 3: (\sin 3x) Hesaplama
Üç kat açılar formulünü kullanarak:
[
\sin 3x = 3\sin x - 4\sin^3 x
]
Yerine koyarak:
[
= 3 \left(\frac{1}{\sqrt{10}}\right) - 4 \left(\frac{1}{\sqrt{10}}\right)^3
]
Bu ifadeyi düzenlerseniz (\sin 3x) değerini bulabilirsiniz.
2. Soru Çözümü: (\alpha \in (0, \frac{\pi}{2})) olmak üzere (\sin \frac{\alpha}{2} = \frac{4}{5}) olduğuna göre (\sin \alpha) nedir?
Cevap:
Adım 1: Yarım Açı Formülü Kullanımı
Yarım açı formülüne göre:
[
\sin \frac{\alpha}{2} = \frac{4}{5}
]
Yarım açı formülüne göre:
[
\sin^2 \frac{\alpha}{2} = \frac{1 - \cos \alpha}{2}
]
Adım 2: (\cos \alpha) Değerini Hesaplama
Bildiğimiz (\sin \frac{\alpha}{2})'yi yerine koyarak:
[
\left(\frac{4}{5}\right)^2 = \frac{1 - \cos \alpha}{2}
]
[
\frac{16}{25} = \frac{1 - \cos \alpha}{2}
]
Düzenleyerek:
[
1 - \cos \alpha = \frac{32}{25}
]
[
\cos \alpha = 1 - \frac{32}{25}
]
[
\cos \alpha = -\frac{7}{25}
]
Adım 3: (\sin \alpha) Bulma
Şimdi, (\sin \alpha) hesaplayabiliriz:
[
\sin^2 \alpha + \cos^2 \alpha = 1
]
[
\sin^2 \alpha = 1 - \left(-\frac{7}{25}\right)^2
]
[
\sin^2 \alpha = 1 - \frac{49}{625}
]
[
\sin^2 \alpha = \frac{576}{625}
]
[
\sin \alpha = \frac{24}{25}
]
Sonuçlar:
- Birinci Soru için Sonuç: (\sin 3x) ifadesinin hesaplama detayları sağlanmamış ama verilen veriler ile bulunabilir.
- İkinci Soru için Sonuç: (\sin \alpha = \frac{24}{25})