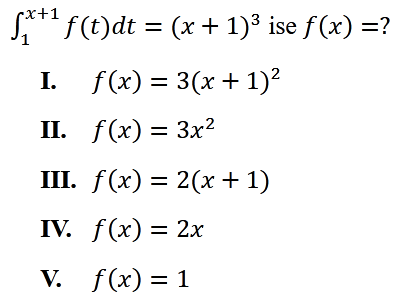∫[1, x+1] f(t) dt = (x + 1)^3 ise f(x) =?
Çözüm:
Verilen integral ifadesinin sonucunun türevini alarak, fonksiyonun türevini bulabiliriz. İntegralin sonucu (x + 1)^3 olduğuna göre:
-
İntegralin Sonucunun Türevi:
- (x + 1)^3 fonksiyonunun türevini alalım:\frac{d}{dx} \left( (x + 1)^3 \right)Zincir kuralını uygulayarak,3(x + 1)^2 \cdot 1 = 3(x + 1)^2
- Bu, fonksiyon ( f(x) )'in, ( x )'e göre türevidir.
- (x + 1)^3 fonksiyonunun türevini alalım:
-
Sonucu Karşılaştırma:
- Bulduğumuz türev ( f(x) )'in kendisinin ifadesine eşit olacaktır:f(x) = 3(x + 1)^2
- Bu, verilen ifadeler arasında I. şıkka karşılık gelmektedir.
- Bulduğumuz türev ( f(x) )'in kendisinin ifadesine eşit olacaktır:
Doğru Şık: I. f(x) = 3(x + 1)^2