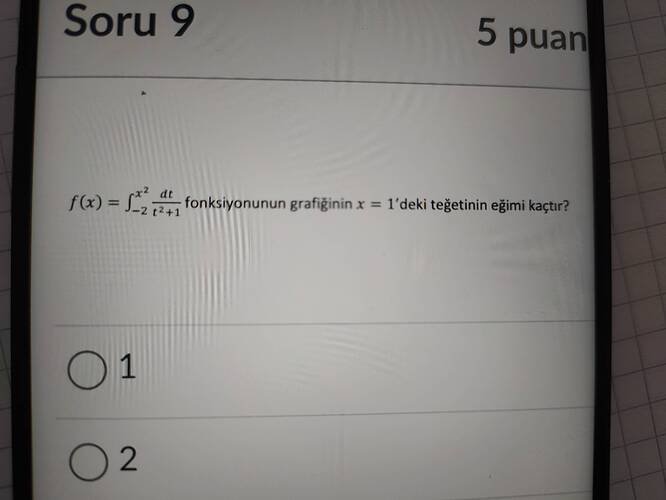
( f(x) = \int_{-2}^{x} \frac{t^2}{t^2+1} , dt ) fonksiyonunun grafiğinin ( x = 1 )'deki teğetinin eğimi kaçtır?
Cevap:
Bir fonksiyonun grafiğinin bir noktadaki teğetinin eğimi, o noktadaki türevdir. Burada ( f(x) ) fonksiyonunun ( x = 1 ) noktasındaki türevini bulmamız gerekiyor.
Öncelikle, verilen integral formülüne göre ( f(x) ) fonksiyonunu yazalım:
[ f(x) = \int_{-2}^{x} \frac{t^2}{t^2+1} , dt ]
Bu tür fonksiyonların türevini hesaplamak için Leibniz integrasyon kuralını kullanabiliriz:
[ f’(x) = \frac{d}{dx} \left( \int_{-2}^{x} g(t) , dt \right) = g(x) ]
Burada ( g(x) ) integrand fonksiyonudur:
[ g(t) = \frac{t^2}{t^2+1} ]
O zaman, ( f(x) ) fonksiyonunun türevi ( g(x) ) olacaktır:
[ f’(x) = \frac{x^2}{x^2+1} ]
Şimdi, ( x = 1 ) noktasındaki türevini bulalım:
[ f’(1) = \frac{1^2}{1^2+1} = \frac{1}{2} ]
Dolayısıyla, ( f(x) ) fonksiyonunun grafiğinin ( x = 1 )'deki teğetinin eğimi (\boxed{\frac{1}{2}})'dir.
Sonuç:
Grafiğin ( x = 1 )'deki teğetinin eğimi (\boxed{1}) değil, (\boxed{\frac{1}{2}}) olacaktır.