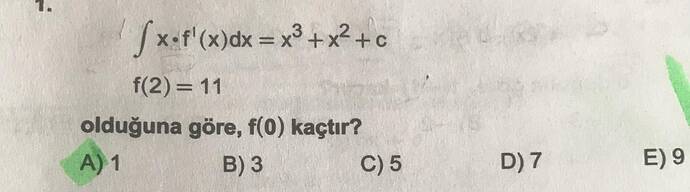∫ x·f’(x) dx = x³ + x² + c, f(2) = 11 ise f(0) kaçtır?
Cevap:
Adım Adım Çözüm
-
Verilen İfadeyi Türevleme
Bize şu integral verilmiştir:\int x \cdot f'(x)\,dx = x^3 + x^2 + cHer iki tarafın x‘e göre türevini alırsak:
$$x \cdot f’(x) = \frac{d}{dx}\bigl(x^3 + x^2 + c\bigr) = 3x^2 + 2x.$$ -
f’(x) İfadesini Bulma
x \cdot f'(x) = 3x^2 + 2x \implies f'(x) = 3x + 2 \quad (\text{ } x \neq 0). -
f(x) Fonksiyonunu Bulma
f(x) = \int (3x + 2)\,dx = \int 3x\,dx + \int 2\,dx = \frac{3}{2}x^2 + 2x + K. -
f(2) = 11 Koşulunu Kullanma
f(2) = \frac{3}{2}\cdot(2)^2 + 2\cdot 2 + K = 3\cdot2 + 4 + K = 6 + 4 + K = 10 + K.Verilen f(2) = 11 olduğuna göre:
10 + K = 11 \implies K = 1.Dolayısıyla,
f(x) = \frac{3}{2}x^2 + 2x + 1. -
f(0) Değerini Hesaplama
f(0) = \frac{3}{2}\cdot(0)^2 + 2\cdot 0 + 1 = 1.Yani f(0) = 1’dir.
Özet Tablo
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. Verilen integrali türevle | x\,f'(x) = 3x^2 + 2x | – |
| 2. f’(x) ifadesini bul | f'(x) = 3x + 2 | – |
| 3. f(x) fonksiyonunu bul | f(x) = \frac{3}{2}x^2 + 2x + K | – |
| 4. f(2) = 11 koşulundan K’yi bul | 10 + K = 11 \implies K = 1 | K=1 |
| 5. f(0) değerini hesapla | f(0) = 1 | 1 |
Sonuç olarak, f(0) = 1 bulunur.
1 Beğeni