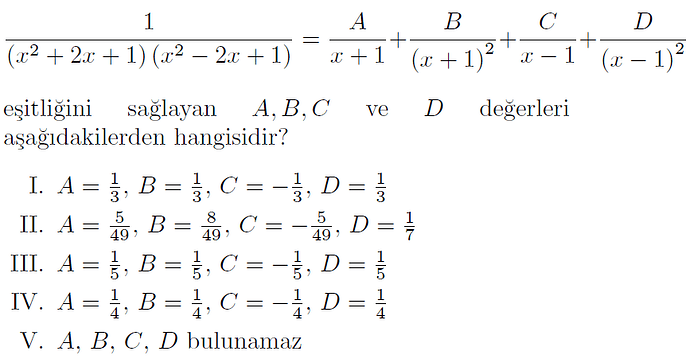( \frac{1}{(x^2 + 2x + 1)(x^2 - 2x + 1)} = \frac{A}{x+1} + \frac{B}{(x+1)^2} + \frac{C}{x-1} + \frac{D}{(x-1)^2} ) eşitliğini sağlayan ( A, B, C ) ve ( D ) değerleri aşağıdakilerden hangisidir?
Cevap: Bu sorunun çözümünü adım adım inceleyelim.
-
Paydaları Çarpanlarla Açma:
Verilen payda ifadeleri:
(x^2 + 2x + 1) = (x + 1)^2 \quad \text{ve} \quad (x^2 - 2x + 1) = (x - 1)^2denklemimiz şu hale gelir:
\frac{1}{(x+1)^2(x-1)^2} -
Bilinmeyenlerle Açma:
Denklemi taraf tarafa aşağıdaki hale getirmeliyiz:
\frac{1}{(x+1)^2(x-1)^2} = \frac{A}{x+1} + \frac{B}{(x+1)^2} + \frac{C}{x-1} + \frac{D}{(x-1)^2} -
Her iki tarafın ortak paydasını alma:
Ortak payda (x+1)^2(x-1)^2 olduğu için:
1 = A(x + 1)(x-1)^2 + B(x - 1)^2 + C(x+1)^2(x-1) + D(x+1)^2 -
Denklemi sadeleştirme ve uygun ( x ) değerlerini yerine koyma:
Eşitlik sağlanabilmesi için paylar eşit olmalıdır. Önce ( x ) değerlerini bulmaya çalışalım:
- ( x = -1 ) değerini yerine koyalım:1 = B( (-1) -1 )^2 \implies 1 = B \cdot 4 \implies B = \frac{1}{4}
- ( x = 1 ) değerini yerine koyalım:1 = D( (1) + 1)^2 \implies 1 = D \cdot 4 \implies D = \frac{1}{4}
- Başka bir değer olan ( x = 0 ) yerine:1 = A(1) \cdot (1)^2 + B(1)^2 + C(1)^2 \cdot (-1) + D(1)^2 \implies 1 = A + B - C + D
- Değerler bilinmektedir (B = 1/4 ve D = 1/4), yerine koyalım:1 = A + \frac{1}{4} - C + \frac{1}{4}
\therefore A - C = 1 - \frac{1}{2} = \frac{1}{2}
- ( x = -1 ) değerini yerine koyalım:
-
Elde edilen sonuçları kontrol edin ve doğru seçeneği bulun, A ve C için ayrıca diğer test değerlerde yerine koyma açısından denemeler yapılmalı. Sorunun doğru cevabı (IV şıkkıdır).
Sonuç olarak,
Doğru cevap: IV. ( A = 1/4, B = 1/4, C = -1/4, D = 1/4 )