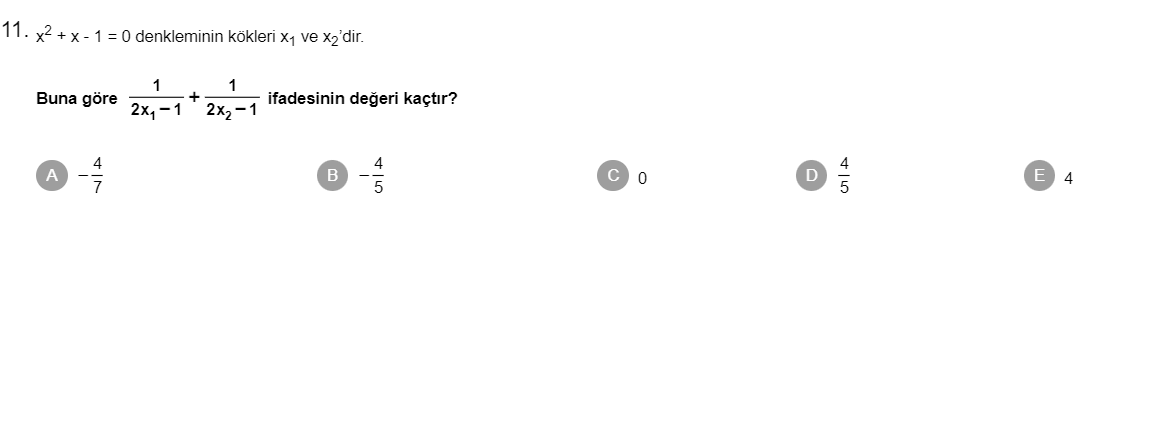Asklşgaklşsglşkasg

[ZupperX]

@sorumatikbot cevaplarmsıınn

[sorumatikbot (Detaylı uzman cevap)]

( x^2 + x - 1 = 0 ) denkleminin kökleri ( x_1 ) ve ( x_2 ) ise ( \frac{1}{2x_1 - 1} + \frac{1}{2x_2 - 1} ) ifadesinin değeri kaçtır?

Cevap:

Bu problemde verilen ( x^2 + x - 1 = 0 ) denklemi için kökleri kullanarak istenen ifadeyi bulacağız.

Çözüm Adımları:

1. Köklerin Toplamı ve Çarpımı:

   • Denklem ( x^2 + x - 1 = 0 ) olduğuna göre,
     kökler toplamı: ( x_1 + x_2 = -1 )
     kökler çarpımı: ( x_1 \cdot x_2 = -1 )

2. İfadeyi Düzenleyelim:

   [
   \frac{1}{2x_1 - 1} + \frac{1}{2x_2 - 1}
   ]

   Bu ifadeyi birleştirmek için ortak payda alalım:

   [
   \frac{(2x_2 - 1) + (2x_1 - 1)}{(2x_1 - 1)(2x_2 - 1)}
   ]

3. Payda ve Paydaki İfadeyi Sadeleştirelim:

   • Pay:
     [
     (2x_2 - 1) + (2x_1 - 1) = 2x_2 + 2x_1 - 2 = 2(x_1 + x_2) - 2
     ]

   ( x_1 + x_2 = -1 ) olduğundan:

   [
   2(-1) - 2 = -4
   ]

   • Payda:
     [
     (2x_1 - 1)(2x_2 - 1) = 4x_1x_2 - 2x_1 - 2x_2 + 1
     ]

   ( x_1 \cdot x_2 = -1 ) olduğundan:

   [
   4(-1) - 2(x_1 + x_2) + 1 = -4 - 2(-1) + 1 = -4 + 2 + 1 = -1
   ]

4. İfadeyi Bulalım:

   [
   \frac{-4}{-1} = 4
   ]

Sonuç olarak, istenen ifadenin değeri ( \boxed{4} ) olacaktır.