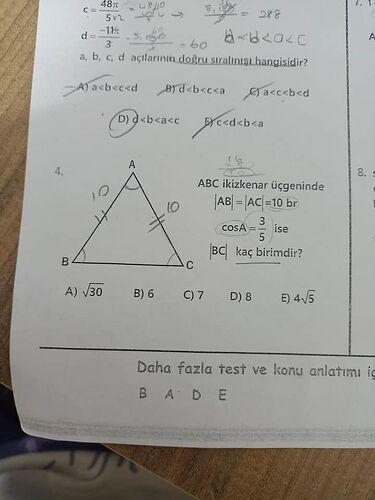
ABC ikizkenar üçgeninde (|AB| = |AC| = 10 \text{ br} ) ve (\cos A = \frac{3}{5}) ise (|BC|) kaç birimdir?
Çözüm:
Verilen üçgen (\triangle ABC) ikizkenar bir üçgen ve (|AB| = |AC| = 10 \text{ br} ). Ayrıca, (\cos A = \frac{3}{5}) verilmiş, bu nedenle trigonometrik özellikleri kullanarak (|BC|)'yi bulabiliriz.
Adımlar:
-
Kosinus Teoremi Uygulaması:
Kosinus teoremi üçgenlerle ilgilidir ve şu şekilde ifade edilir:
[
c^2 = a^2 + b^2 - 2ab \cdot \cos(C)
]Burada (|AB| = |AC| = a = b = 10 \text{ br} ) ve ( C ) açısı yerine ( A ) açısını kullanırsak:
[
|BC|^2 = 10^2 + 10^2 - 2 \cdot 10 \cdot 10 \cdot \left(\frac{3}{5}\right)
] -
Hesaplamalar:
[
|BC|^2 = 100 + 100 - 200 \cdot \frac{3}{5}
][
|BC|^2 = 200 - 120
][
|BC|^2 = 80
][
|BC| = \sqrt{80} = \sqrt{16 \cdot 5} = 4\sqrt{5}
]
Sonuç:
Doğru cevap E şıkkı: (4\sqrt{5}).