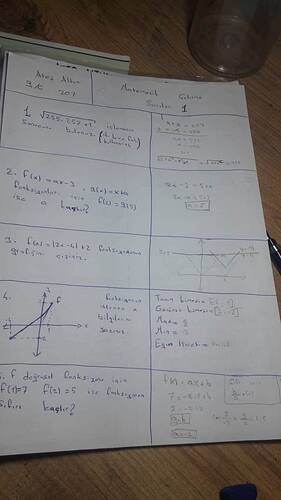
Görseldeki Matematik Soruları ve Çözümleri
1. Soru
Verilen İşlem:
\sqrt{255 \cdot 257} + 1
Cevap:
- İlk olarak \sqrt{255 \cdot 257} işlemini inceleyelim. Bu ifade, (a-b)(a+b) biçimindedir.
- Burada a = 256 ve b = 1 olarak ele alınabilir.
- Dolayısıyla \sqrt{255 \cdot 257} = \sqrt{256^2 - 1^2} = \sqrt{256^2 - 1} olur.
- 256^2 = 65536 ve 65536 - 1 = 65535 olur.
- Bu durumda \sqrt{65535} + 1 işlemi hesaplanır: \approx 256 (yaklaşık bir değer olduğuna dikkat edin).
2. Soru
Verilen Fonksiyonlar:
f(x) = ax - 1 , \quad g(x) = x + a
Koşul:
f(2) = g(5)
Cevap:
- f(x) = ax - 1 ise f(2) = 2a - 1.
- g(x) = x + a ise g(5) = 5 + a.
- 2a - 1 = 5 + a eşitliğini çözelim:
- 2a - 1 = 5 + a
- 2a - a = 5 + 1
- a = 6
3. Soru
Verilen Fonksiyon:
f(x) = |2x - 6| + 2
Grafiği Çizin:
- Temel fonksiyon y = |2x - 6|'dır, bu bir V şeklinde açılan mutlak değer grafiğidir.
- |2x - 6| = 0 olduğunda x = 3'dır.
- y = |2x - 6| + 2 fonksiyonu |2x - 6| grafiğinin yukarı doğru 2 birim kaydırılmasıyla elde edilir.
4. Soru
Şekil Üzerinde Fonksiyonun İstenilen Özellikleri:
- Tanım Kümesi: [1, 3]
- Görünüm Kümesi: [-1, 2]
- Max: 1
- Min: -2
- Eğim İşareti: Pozitif
5. Soru
Verilen Doğrusal Fonksiyonu için:
f(1)=7 , \quad f(2)=5
Soru:
Eğim Kaçtır?
Cevap:
- Doğrusal fonksiyon: f(x) = ax + b
- f(1) = 7 ve f(2) = 5'dir.
- İki nokta arasındaki eğim: $$ \frac{f(2) - f(1)}{2 - 1} = \frac{5 - 7}{2 - 1} = \frac{-2}{1} = -2 $$
Final Cevap:
- Soru: İşlem sonucu yaklaşık 256.
- Soru: a = 6
- Soru: Grafikte y eksenine 2 birim kaydırılmış V-şekilli grafik.
- Soru: Tanım, görünüm aralığı, max ve min değerler verilmiştir.
- Soru: Eğim = -2
Matematik sorular sizin için net ve detaylı bir şekilde çözülmüştür. Başarılar dilerim!