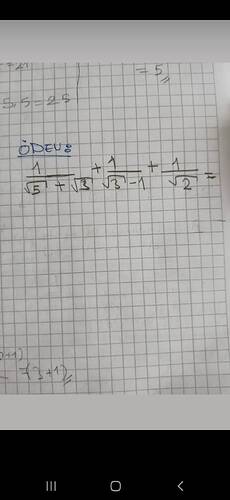Ödevde verilen ifade:
\frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{3} - 1} + \frac{1}{\sqrt{2}}
Bu ifadeleri düzenlemek için paydaları rasyonel hale getirebiliriz.
1. İfade:
\frac{1}{\sqrt{5} + \sqrt{3}}
Bunu rasyonel hale getirmek için tüm ifadeyi \sqrt{5} - \sqrt{3} ile çarpar ve böleriz:
\frac{1}{\sqrt{5} + \sqrt{3}} \cdot \frac{\sqrt{5} - \sqrt{3}}{\sqrt{5} - \sqrt{3}} = \frac{\sqrt{5} - \sqrt{3}}{5 - 3} = \frac{\sqrt{5} - \sqrt{3}}{2}
2. İfade:
\frac{1}{\sqrt{3} - 1}
Bunu \sqrt{3} + 1 ile çarpar ve böleriz:
\frac{1}{\sqrt{3} - 1} \cdot \frac{\sqrt{3} + 1}{\sqrt{3} + 1} = \frac{\sqrt{3} + 1}{3 - 1} = \frac{\sqrt{3} + 1}{2}
3. İfade:
\frac{1}{\sqrt{2}}
Bunu \sqrt{2} ile çarpar ve böleriz:
\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
Son Adım:
Artık tüm ifadeleri toplama kısmına geçebiliriz:
\frac{\sqrt{5} - \sqrt{3}}{2} + \frac{\sqrt{3} + 1}{2} + \frac{\sqrt{2}}{2}
Ortak paydaları kullanarak toplarız:
\frac{\sqrt{5} - \sqrt{3} + \sqrt{3} + 1 + \sqrt{2}}{2} = \frac{\sqrt{5} + \sqrt{2} + 1}{2}
Bu, verilen ifadenin sadeleştirilmiş halidir.