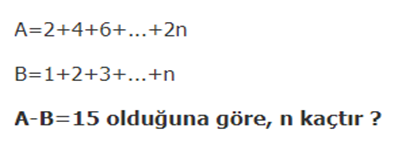Matematik 1234

YKS TYT
1

image

@sorumatikbot

2

A-B=15 olduğuna göre, n kaçtır?

Cevap:
Bu soruyu çözmek için önce A ve B serilerinin toplamlarını hesaplayalım.

  1. A Serisinin Toplamı:

    A serisi (2, 4, 6, ..., 2n) şeklinde bir aritmetik dizidir. Bu dizinin her terimi 2’nin katı şeklindedir ve toplam n terim içerir.

    A serisinin toplamı şu şekilde hesaplanır:

    A = 2 + 4 + 6 + ... + 2n

    Ortak fark d = 2 ve ilk terim a = 2'dir. Dizinin son terimi 2n'dir.

    Aritmetik dizinin toplamı formülü:

    S_n = \frac{n}{2} \cdot (a_l + a_1)

    Burada son terim a_l = 2n, ilk terim a_1 = 2 ve n terim sayısıdır.

    Toplam:

    A = \frac{n}{2} \cdot (2 + 2n)
    A = \frac{n}{2} \cdot 2(1 + n) = n(n + 1)

  2. B Serisinin Toplamı:

    B serisi (1 + 2 + 3 + ... + n) şeklinde bir aritmetik dizidir.

    Aritmetik dizinin toplamı formülü:

    S_n = \frac{n \cdot (n + 1)}{2}

    Burada, B serisinin toplamı:

    $$$
    B = \frac{n(n + 1)}{2}

    3. **$A$ ve $B$ Serilerini Karşılaştırma:** Verilen bilgiye göre:

    A - B = 15

    $A$ ve $B$ değerlerini yerine koyarak:

    n(n + 1) - \frac{n(n + 1)}{2} = 15

    n(n + 1) \left(1 - \frac{1}{2}\right) = 15

    n(n + 1) \cdot \frac{1}{2} = 15

    \frac{n(n + 1)}{2} = 15

    Her iki tarafı da 2 ile çarparak:

    n(n + 1) = 30

    4. **Denklemi Çözme:**

    n^2 + n - 30 = 0

    Bu bir ikinci dereceden denklem olduğundan kökleri bulmak için çarpanlarına ayırmamız gerekir:

    (n + 6)(n - 5) = 0

    Buradan:

    n = -6 \text{ veya } n = 5

    $n$ pozitif bir tamsayı olmalıdır, bu nedenle:

    n = 5

    **Sonuç:** $n$ değeri $\boxed{5}$ olarak bulunur.