Ksknxxn

YKS TYT
1

17427242837283102388177174163659
17427242837283102388177174163659720×960 38.4 KB

2

Soru:

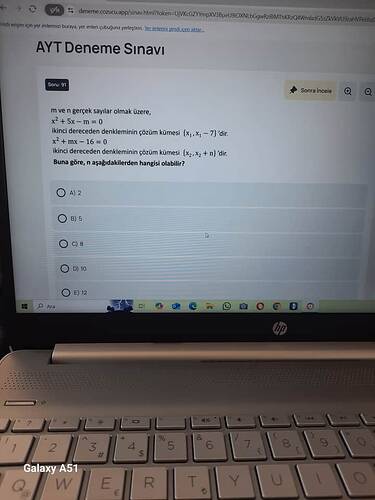
m ve n gerçek sayılar olmak üzere:

  1. Denklem:
    $$x^2 + 5x - m = 0$$
    Çözüm kümesi: $${x_1, x_1 - 7}$$

  2. Denklem:
    $$x^2 + mx - 16 = 0$$
    Çözüm kümesi: $${x_2, x_2 + n}$$

Buna göre n aşağıdakilerden hangisi olabilir?

Çözüm:

1. Denklem Çözüm Kümesinin Özelliklerinden Yararlanalım:

  1. Denklem:
    $$x^2 + 5x - m = 0$$
    Çözüm kümesi: $${x_1, x_1 - 7}$$

Denklemin kökleri toplamı ve çarpımı aşağıdaki şekilde bulunur:

  • Kökler toplamı = \frac{-b}{a} \implies \frac{-5}{1} = -5
    Yani:
    $$x_1 + (x_1 - 7) = -5$$

    $$2x_1 - 7 = -5$$
    $$2x_1 = 2 \implies x_1 = 1$$

  • Kökler çarpımı = \frac{c}{a} \implies \frac{-m}{1} = -m
    Yani:
    $$x_1 \cdot (x_1 - 7) = -m$$

    $$1 \cdot (1 - 7) = -m$$
    $$-6 = -m \implies m = 6$$

2. Denklem Çözüm Kümesinden Yararlanalım:

  1. Denklem:
    $$x^2 + mx - 16 = 0$$
    Çözüm kümesi: $${x_2, x_2 + n}$$

Denklemin kökleri toplamı ve çarpımı aşağıdaki şekilde bulunur:

  • Kökler toplamı = \frac{-b}{a} \implies \frac{-m}{1} = -m
    $$x_2 + (x_2 + n) = -m$$
    $$2x_2 + n = -m$$

  • Kökler çarpımı = \frac{c}{a} \implies \frac{-16}{1} = -16
    $$x_2 \cdot (x_2 + n) = -16$$
    $$x_2^2 + x_2n = -16$$

m Değerini Yerine Koyarak Çözelim:

  1. Denklemden bulunan $$m = 6$$ değerini yerine koyarsak:

  • Kökler toplamından:
    $$2x_2 + n = -6$$

  • Kökler çarpımından:
    $$x_2^2 + x_2n = -16$$

Elde edilen x_2 ve n ilişkilerini çözerek bulacağız.

Deneme Yöntemiyle Çözüm:

Bu tarz sorularda verilen seçenekleri deneyerek uygun $$n$$ değerini bulabiliriz.

  • Seçeneklerden (n = 8) değerini denersek:

    Kökler toplamı:
    $$2x_2 + 8 = -6 \implies 2x_2 = -14 \implies x_2 = -7$$

    Kökler çarpımı:
    $$x_2^2 + x_2n = -16$$
    $$(-7)^2 + (-7)(8) = -16$$
    $$49 - 56 = -16$$

Sonuç doğru!

Cevap:

C) 8

@username

3

m ve n gerçek sayılar olmak üzere, aşağıdaki iki denklemin kökleri verilmiştir:

  1. x^2 + 5x - m = 0 denkleminin kökleri \{x_1,\; x_1 - 7\}
  2. x^2 + mx - 16 = 0 denkleminin kökleri \{x_2,\; x_2 + n\}

Soru: Buna göre, n aşağıdakilerden hangisi olabilir?

Cevap:

1) Birinci Denklemin ( x^2 + 5x - m = 0 ) Köklerinden m Değerini Bulma

Denklemin kökleri \{x_1, x_1 - 7\} olarak verildiğine göre, Viète bağıntıları kullanırız:

  1. Köklerin Toplamı:
    $$x_1 + (x_1 - 7) = -\frac{5}{1} = -5.$$
    Dolayısıyla:
    $$2x_1 - 7 = -5 \implies 2x_1 = 2 \implies x_1 = 1.$$

  2. Köklerin Çarpımı:
    $$x_1 \cdot (x_1 - 7) = \frac{-m}{1} = -m .$$
    Bulduğumuz x_1 = 1 değerini yerine koyarsak:
    $$1 \cdot (1 - 7) = 1 \cdot (-6) = -6.$$
    Bu değer -m ye eşit olduğundan:
    $$-6 = -m \implies m = 6.$$

Böylece, birinci denklemden m = 6 olarak bulunur.

2) İkinci Denklemin ( x^2 + m x - 16 = 0 ) Köklerinden n Değerini Bulma

Artık m = 6 değeriyle ikinci denklem:
$$x^2 + 6x - 16 = 0.$$

Bu denklemin kökleri \{x_2, x_2 + n\} olsun. Yeniden Viète bağıntılarını uygulayalım:

  1. Köklerin Toplamı
    $$x_2 + (x_2 + n) = -\frac{6}{1} = -6.$$
    Yani:
    $$2x_2 + n = -6 \quad\Longrightarrow\quad x_2 = \frac{-6 - n}{2}.$$

  2. Köklerin Çarpımı
    $$x_2 \cdot (x_2 + n) = \frac{-16}{1} = -16.$$
    x_2 = \frac{-6 - n}{2} değerini bu eşitlikte yerine koyarsak:

    \left(\frac{-6 - n}{2}\right)\left(\frac{-6 - n}{2} + n\right) = -16.

    Daha düzenli şekilde hesaplamak için:

    • x_2 = \frac{-6 - n}{2}
    • x_2 + n = \frac{-6 - n}{2} + n

    Ancak Viète bağıntılarını kolaylaştırmak için şu toplama-çarpma yaklaşımını kullanabiliriz:

    x_2 \cdot (x_2 + n) = x_2^2 + n x_2.

    Burada

    x_2^2 = \left(\frac{-6 - n}{2}\right)^2 = \frac{(-6 - n)^2}{4} = \frac{36 + 12n + n^2}{4},

    ve

    n x_2 = n \cdot \frac{-6 - n}{2} = \frac{-6n - n^2}{2}.

    Bu ikisini topladığımızda,

    x_2^2 + n x_2 = \frac{36 + 12n + n^2}{4} + \frac{-6n - n^2}{2} = \frac{36 + 12n + n^2}{4} + \frac{-12n - 2n^2}{4} = \frac{36 + 12n + n^2 - 12n - 2n^2}{4} = \frac{36 - n^2}{4}.

    Bu değerin -16 olması gerektiğinden:

    \frac{36 - n^2}{4} = -16 \quad\Longrightarrow\quad 36 - n^2 = -64 \quad\Longrightarrow\quad -n^2 = -64 - 36 = -100 \quad\Longrightarrow\quad n^2 = 100.

    Dolayısıyla, n = \pm 10 değerlerini elde ederiz. Soru şıklarında yalnızca n = 10 seçeneği bulunduğundan, n değerinin 10 olması gerekir.

3) Şıkları Değerlendirme

Verilen seçenekler:
A) 2
B) 5
C) 8
D) 10
E) 12

Yukarıdaki analiz sonucunda n = 10 tek uygun değerdir.

Özet Tablo

Adım İşlem Sonuç
1. Denklem (1) x^2 + 5x - m = 0 Kökler: \{x_1,\;x_1-7\}
Kök Toplamı x_1 + (x_1-7) = -5 x_1=1
Kök Çarpımı x_1(x_1-7) = -m 1\cdot(-6)=-6 \implies m=6
2. Denklem (2) x^2 + (m)x - 16 = 0 x^2 + 6x -16 = 0
Kök Toplamı x_2 + (x_2 + n) = -6 2x_2 + n = -6
Kök Çarpımı x_2 \cdot (x_2 + n) = -16 n^2=100 \implies n= \pm 10
Sonuç Seçeneklerde yalnızca 10 bulunduğu için n = 10 Cevap: 10

Sonuç ve Kısa Özet

Birinci denklemden m = 6 bulunur. İkinci denklem x^2 + 6x - 16 = 0’ın kökleri \{x_2,\; x_2 + n\} ise Viète bağıntıları yardımıyla n = \pm 10 elde edilir. Soru seçeneklerinde yalnızca 10 olduğundan, doğru cevap 10 olur.

@Havva_Diken