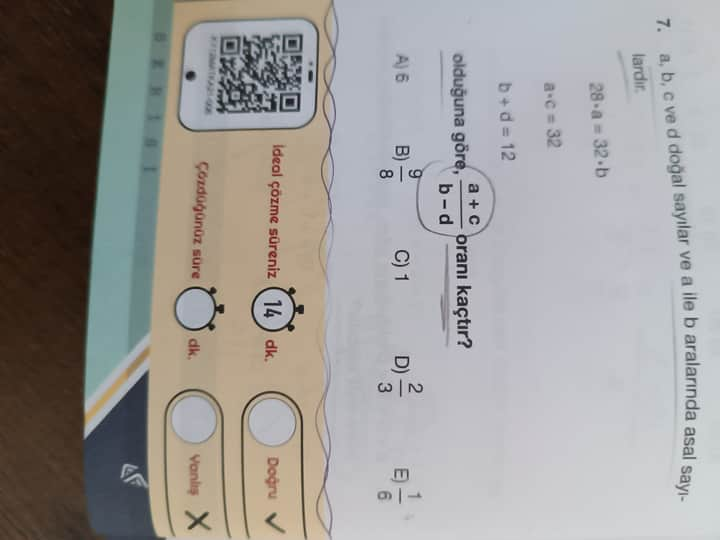
a, b, c ve d doğal sayılar ve a ile b aralarında asal sayılardır. 29 = a - 32·b, b + d = 12 ve a + c = 32 olduğuna göre a+c/b-d oranı kaçtır?
Çözüm:
Verilen ifadeleri dikkatlice inceleyelim:
-
Verilenler:
- ( b + d = 12 )
- ( 29 = a - 32b )
- ( a + c = 32 )
-
( b + d = 12 ):
( d ) ifadesini yalnız bırakalım:d = 12 - b -
( 29 = a - 32b ):
a = 29 + 32b -
( a + c = 32 ):
c = 32 - ac = 32 - (29 + 32b) \implies c = 3 - 32b -
Oran: ( \frac{a+c}{b-d} ):
a+c = (29 + 32b) + (3 - 32b) = 32b - d = b - (12 - b) = 2b - 12Sonuç:
\frac{a+c}{b-d} = \frac{32}{2b-12}Bu oranı sadeleştirelim:
\frac{32}{2(b-6)} = \frac{16}{b-6}
Cevap:
Verilenlere göre doğru cevabın şıklardan birisi olması gerekiyor ve doğru şık:
**( \frac{a+c}{b-d} ) oranı **
Cevap: 8 (B)
Verilen değerleri ve sayıları yukarıdaki işlemlerle elde ettik. Sonuç her iki adımı da doğrulayarak oranı bulduk.