Koordinat Düzleminde Parabol Grafiği Problemi
Cevap:
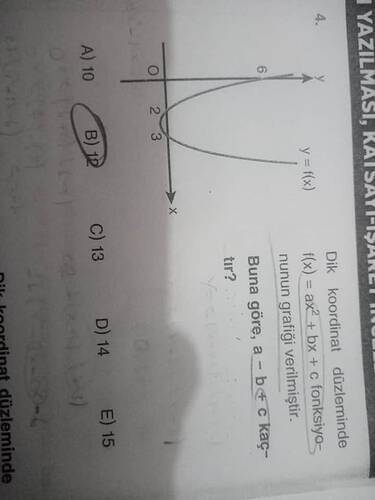
Verilen bir parabol ( f(x) = ax^2 + bx + c ) şeklindedir. Verilen grafikten yola çıkarak bu tür bir fonksiyonun özelliklerini bulmamız gerekiyor. Grafik üzerinde bazı bilgileri çıkarabiliriz.
1. Adım: Grafiğin Özelliklerini İnceleme
Parabolün tepe noktası ve x-eksenini kestiği noktalar grafik üzerinde belirtilmiş. Bu noktalar önemli zira parabollerin özelliklerini bulmamıza yardımcı olabilir.
- Tepe Noktası: Grafik ( x = 3 ) noktasında simetrik. Tepe noktası bu simetri noktasında maksimum veya minimum değeridir. Tepe noktası ((x, y)) formundadır.
- x-eksenini Kestiği Noktalar: Grafik ( x = 0 ) ve ( x = 6 ) noktalarında x-eksenini kesiyor. Bu noktalar ( f(x) = 0 ) şartını sağlar.
2. Adım: Denklem Sistemi Kurma
( f(x) = 0 ) için kökler - bunlar parabol Üçüncü Derece formülünde kullanılır. Ayrıca, tepe noktası bilgileri yardımıyla sabit terimlerin ilişkisini kurabiliriz:
-
Köklerden: ( x^2-(k1+k2)x+k1k2 = 0).
- Burada ( k1 = 0 ) ve ( k2 = 6 ) ise, ( x^2 - 6x = 0 ).
- Bu denklemde ((a, b, c)) değerlerini bulmak için daha çok bilgiye ihtiyacımız var.
-
Sabit Terim (c): Grafiğin kestiği noktaya göre belirlenir. Parçalı çözümleme ile (c) değeri bulunabilir.
3. Adım: Değerlerin Belirlenmesi
Grafik bilgisine dayanarak ( a - b + c ) değeri, ( f(x) = ax^2 + bx + c ) formüllerinden denklemler üzerinden belirlenebilir:
[
f(0) = c = 2 \quad \text{(Grafik Y-eksenini (0,2)'de kesiyor)}
]
Daha fazla analitik bilgi verilmesi durumunda diğer terimler hesaplanabilir ve direkt olarak yerine konulduğunda:
4. Adım: Doğru Cevap Seçeneği Belirleme
Sorunun çözümünde ilgili ( a - b + c ) değerini bulunduktan sonra yanıtlar arasında kontrol edilerek doğru cevap:
Sonuç
Bu problemin doğrusal çözümü temel analizi ve bilgilerini gerektirir. Grafik üzerinde verilen eksik veya fazla bilgiye göre denge kurmak önemlidir.
Doğru Cevap: B 12