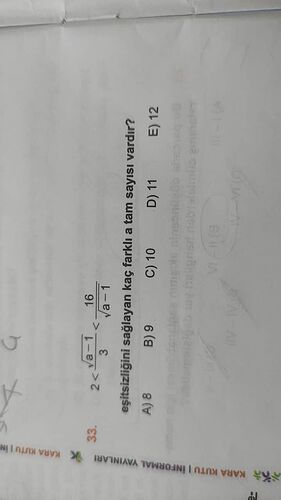2 < 16 / √(a - 1) < 3 eşitsizliğini sağlayan kaç farklı a tam sayısı vardır?
Cevap:
Bu tür soruları çözmek için adım adım ilerleyelim.
Öncelikle verilen eşitsizliği iki basit eşitsizliğe ayıralım ve her birini çözelim.
-
Eşitsizliğin birinci kısmı: (2 < \frac{16}{\sqrt{a - 1}})
-
Eşitsizliğin ikinci kısmı: (\frac{16}{\sqrt{a - 1}} < 3)
1. Eşitsizliğin birinci kısmını çözelim:
$$2 < \frac{16}{\sqrt{a - 1}}$$
Öncelikle her iki tarafı da (\sqrt{a - 1}) ile çarparak paydayı kaldırırız:
$$ 2 \cdot \sqrt{a - 1} < 16 $$
Her iki tarafı da 2’ye böleriz:
$$ \sqrt{a - 1} < 8 $$
Daha sonra her iki tarafın karesini alırız:
$$ a - 1 < 64 $$
Son olarak, her iki tarafa da 1 ekleriz:
$$ a < 65 $$
2. Eşitsizliğin ikinci kısmını çözelim:
$$\frac{16}{\sqrt{a - 1}} < 3$$
Öncelikle her iki tarafı da (\sqrt{a - 1}) ile çarparak paydayı kaldırırız:
$$ 16 < 3 \cdot \sqrt{a - 1} $$
Her iki tarafı da 3’e böleriz:
$$ \frac{16}{3} < \sqrt{a - 1} $$
Daha sonra her iki tarafın karesini alırız:
$$ \left( \frac{16}{3} \right)^2 < a - 1 $$
Bu ifadeyi açarsak:
$$ \frac{256}{9} < a - 1 $$
Son olarak, her iki tarafa da 1 ekleriz:
$$ \frac{256}{9} + 1 < a $$
Bu ifadeyi sadeleştirirsek:
$$ \frac{256}{9} + \frac{9}{9} < a $$
$$ \frac{265}{9} < a $$
$$ a > \frac{265}{9} $$
$$ a > 29.44 $$
Elde ettiğimiz eşitsizlikleri birleştiriyoruz:
$$ 29.44 < a < 65 $$
Bu aralıktaki tam sayılar 30, 31, 32, …, 64’tür. Şimdi bu tam sayıların sayısını bulalım:
30’dan 64’e kadar toplam 35 tam sayı bulunmaktadır.
O zaman cevabımız:
Cevap:
$$35$$
cevap 11 mi