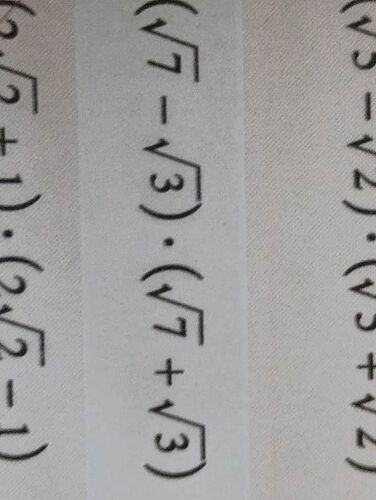Görseldeki ifadeyi çarparken kök içindeki sayıları çarpma işlemi yapacağız:
$$(\sqrt{7} - \sqrt{3}) \cdot (\sqrt{7} + \sqrt{3})$$
Bu çarpım, bir özdeşlik olan “iki kare farkı” özdeşliği ile yapılabilir:
$$(a - b)(a + b) = a^2 - b^2$$
Bu durumda a = \sqrt{7} ve b = \sqrt{3} olduğuna göre:
(\sqrt{7})^2 - (\sqrt{3})^2 = 7 - 3 = 4
Bu nedenle, ifade \boxed{4} olarak sadeleşir.