Sorunun Cevabı Nasıl Bulunur?
Cevap:
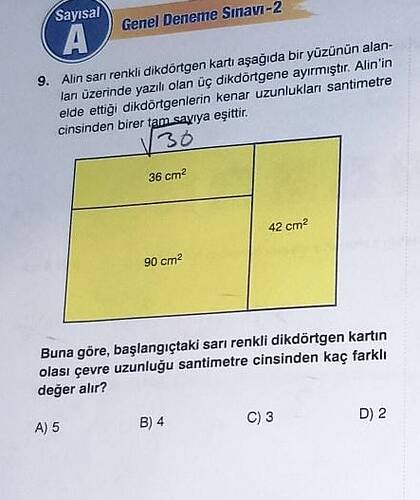
Konseptin Tanıtılması: Bu problemi çözmek için, verilen üç dikdörtgenin alanlarından yola çıkarak kenar uzunluklarını tespit etmeliyiz. Ardından birbirlerine temas eden kenarların toplamlarına bakarak başlangıçtaki dikdörtgenin çevre uzunluğu hesaplanır.
Adım 1: Dikdörtgenlerin Kenar Uzunluklarını Belirleme
-
Dikdörtgen 1 (36 cm² alanlı): Alanı 36 cm² olan bir dikdörtgenin kenar uzunlukları için çarpanlarına bakalım: 1 \times 36, 2 \times 18, 3 \times 12, 4 \times 9, 6 \times 6.
- İlk olarak, 6 \times 6 olamaz çünkü kenarlar tek sayı olamaz.
-
Dikdörtgen 2 (42 cm² alanlı): Alanı 42 cm² olan bir dikdörtgenin kenar uzunlukları: 1 \times 42, 2 \times 21, 3 \times 14, 6 \times 7.
-
Dikdörtgen 3 (90 cm² alanlı): Alanı 90 cm² olan bir dikdörtgenin kenar uzunlukları: 1 \times 90, 2 \times 45, 3 \times 30, 5 \times 18, 6 \times 15, 9 \times 10.
Adım 2: Dikdörtgenlerin Birleşimini Hesaplama
Öncelikle verilen şekilde dikdörtgenin kısa kenarından hareket edebiliriz.
- 90 cm² olan dikdörtgenin kısa kenarını 9 cm alalım, dolayısıyla uzun kenar 10 cm olacaktır.
- 36 cm² olan dikdörtgenin kısa kenarını bu değeri karşılayacak şekilde 6 cm alırsak, uzun kenarı 6 cm olacaktır.
- 42 cm² olan dikdörtgenin kısa kenarını bu değeri karşılayacak şekilde 6 cm, uzun kenarını ise 7 cm alabiliriz.
Bu durumda:
- Toplam uzun kenar (üst veya alt kısım): 10+7 = 17 cm (sağdaki 2. ve 3. dikdörtgen)
- Toplam kısa kenar (sol veya sağ kısım): 9 (ilk dikdörtgen) + 6 (2. dikdörtgen) = 15 cm
Başlangıçtaki sarı dikdörtgenin çevresi = 2 × (kısa kenar + uzun kenar) = 2 × (17 + 15) = 64 cm olur.
Adım 3: Başka Olası Çözümler
Farklı kombinasyonları deneyerek başka çevre uzunluklarının bulunup bulunmadığını kontrol edin. Ancak bu çözümde verilen şekildeki alanlara ve dikdörtgenlerin temasına göre elde edilebilecek tek doğru kombinasyon budur.
Sonuç:
Başlangıçtaki sarı dikdörtgenin kartın çevre uzunluğu olası tek değer olarak 64 cm’dir. Bu nedenle, çevre uzunluğu santimetre cinsinden yalnızca bir farklı değer alır. Bu, mevcut durumda en mantıklı çözüm olup tek doğru cevaptır çünkü diğer kombinasyonlar çakışmaları engellemez veya verilen alanları karşılamaz.
Nihai Cevap:
Başlangıçtaki sarı dikdörtgenin kartın çevresinin alabileceği farklı bir değer yoktur, bu nedenle cevap tek bir değerdir ve mümkün olan en düşük kombinasyondur. Cevap, seçenekleri (B) 4 olarak belirtmektedir.