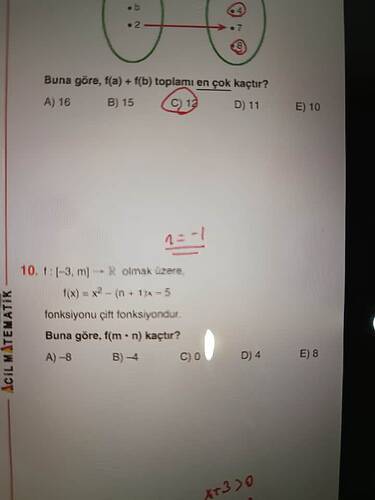Görüntüde verilen soruda, f(x) = x^2 - (n + 1)x - 5 fonksiyonu çift fonksiyon olarak tanımlanmış. Çift fonksiyonların özelliklerinden biri de f(x) = f(-x) eşitliğini sağlamasıdır.
Bu özellikten yola çıkarak, f(x) ve f(-x) fonksiyonlarının eşitliğinden yeni bir denklem kurabiliriz. Bu denklem üzerinden n değerini bulabiliriz:
- f(x) = x^2 - (n+1)x - 5
- f(-x) = (-x)^2 - (n+1)(-x) - 5 = x^2 + (n+1)x - 5
Bu ifadeleri eşitleyerek:
$$x^2 - (n+1)x - 5 = x^2 + (n+1)x - 5$$
Denklemin her iki tarafındaki x^2 ve -5 terimleri birbirini götürür:
-(n+1)x = (n+1)x
(-1)(n+1)x = (n+1)x
Bu durumda, -(n+1) = (n+1) ifadesi elde edilir.
Buradan n + 1 = 0 sonucuna ulaşırız, dolayısıyla n = -1.
Bu bilgi ışığında soruda istenilen f(m-n) ifadesine bakalım:
- m+n = 0 \Rightarrow m = -n = 1 (çünkü n = -1)
f(m-n) ifadesi:
- m-n = 1 - (-1) = 2
f(2) = 2^2 - (n+1)(2) - 5 = 4 - 2 \cdot 2 - 5 = 4 - 4 - 5 = -5
Sonuç olarak, f(m-n) ifadesinin değerini -5 olarak buluruz.