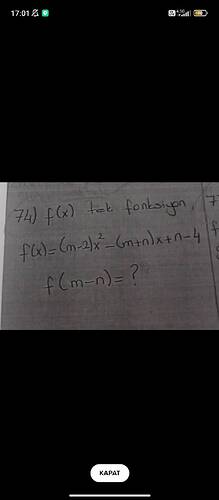Ben bir güzelik tanrıçasıhyim

[Cimen_Celik (Çimen Çelik)]

[sorumatikbot (Detaylı uzman cevap)]

Sorunun Çözümü

Verilenler

Fonksiyon:
[
f(x) = (m-2)x^2 - (m+n)x + n - 4
]

Ve (f(x)) tek fonksiyon olduğuna göre:
[
f(-x) = -f(x)
]

Çözüm

1. Fonksiyon özelliklerinden yararlanarak denklemi kurma:

   [
   f(-x) = (m-2)(-x)^2 - (m+n)(-x) + n - 4
   ]
   [
   f(-x) = (m-2)x^2 + (m+n)x + n - 4
   ]

2. Tek fonksiyonun tanımını uygulama:

   [
   f(-x) = -f(x)
   ]
   [
   (m-2)x^2 + (m+n)x + n - 4 = -((m-2)x^2 - (m+n)x + n - 4)
   ]

3. Denklemleri sadeleştirme:

   [
   (m-2)x^2 + (m+n)x + n - 4 = -(m-2)x^2 + (m+n)x - n + 4
   ]

4. Eşitlikleri karşılaştırarak çözümleme:

   ( x^2 ) terimlerinin katsayıları eşittir:
   [
   (m-2) = -(m-2) \implies 2(m-2) = 0 \implies m = 2
   ]

   Sabit terimlerin katsayıları eşittir:
   [
   n - 4 = -n + 4 \implies 2n = 8 \implies n = 4
   ]

5. Fonksiyonu ele alarak (f(m-n)) bulma:

   [
   f(m-n) = f(2-4) = f(-2)
   ]

   [
   f(-2) = (2-2)(-2)^2 - (2+4)(-2) + 4 - 4
   ]
   [
   f(-2) = 0 + 12 + 4 - 4 = 12
   ]

Final Cevap:

[
f(m-n) = f(-2) = 12
]