Jrzoyzotzo

YKS TYT
1

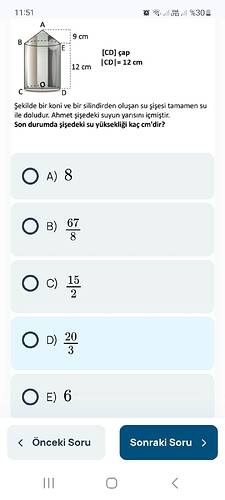
Screenshot_20250308_115130_Chrome
Screenshot_20250308_115130_Chrome720×1600 36.6 KB

2

Görev: Şişedeki suyun yukarıda verilen şekle göre son yükseklik hesabını gerçekleştirme.

Şişe, bir koni ve bir silindirin birleşiminden oluşmaktadır. Silindirin çapı ve yüksekliği verilmiştir; koninin yüksekliği ve çapı da verilmiştir.

Adım 1: İlk Durumdaki Su Hacmini Hesaplama

Şişe başlangıçta tamamen doludur ve içinde bulunan toplam su miktarı, bir koninin hacmi ve bir silindirin hacmi toplamıdır.

Koni ve Silindirin Formülleri

Hacim hesaplaması için kullanılan formüller:

  • Koni Hacmi:
V_k = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h_k

Burada:
r koninin yarıçapı = \frac{\text{çap}}{2} = \frac{12}{2} = 6 \, \text{cm}
h_k koninin yüksekliği = 9 \, \text{cm}

  • Silindir Hacmi:
V_s = \pi \cdot r^2 \cdot h_s

Burada:
r silindirin yarıçapı = 6 \, \text{cm}
h_s silindirin yüksekliği = 12 \, \text{cm}

1. Koni ve Silindir Hacmini Hesaplama

Koni hacmi:

V_k = \frac{1}{3} \cdot \pi \cdot 6^2 \cdot 9 = \frac{1}{3} \cdot \pi \cdot 324 = 108 \pi \, \text{cm}^3

Silindir hacmi:

V_s = \pi \cdot 6^2 \cdot 12 = \pi \cdot 36 \cdot 12 = 432 \pi \, \text{cm}^3

Toplam ilk hacim:

V_{\text{toplam}} = V_k + V_s = 108\pi + 432\pi = 540\pi \, \text{cm}^3

Adım 2: Ahmet Suyun Yarısını İçiyor

Ahmet şişedeki suyun yarısını içiyor. İlk hacmin yarısı:

V_{\text{yarım}} = \frac{540\pi}{2} = 270\pi \, \text{cm}^3

Adım 3: Son Durumdaki Su Yüksekliğini Hesaplama

Şişedeki suyun tamamı ilk başta hem koni hem de silindiri dolduruyordu. Şimdi su miktarı 270π cm³. Bu suyun yüksekliği, önce silindiri tamamen doldurduktan sonra koninin içine taşar.
Hesaplama yapılırken şu iki durumu kontrol edeceğiz:

1. Silindirdeki Su Hacmi

Silindirin dolması için gereken hacim:

V_s = 432\pi \, \text{cm}^3

Su miktarı 270π cm³, bu hacimin tamamını doldurmaya yetmez. Bu yüzden yeni su yüksekliği silindir içindeki miktar üzerinden hesaplanacaktır.

Silindirdeki su hacmi:

V_{\text{silindir}} = \pi \cdot r^2 \cdot h_s

Buradan, son su yüksekliğini çözebiliriz:

h_s = \frac{V_{\text{yarım}}}{\pi \cdot r^2}
h_s = \frac{270\pi}{\pi \cdot 36}
h_s = \frac{270}{36} = 7.5 \, \text{cm}

Sonuç

Ahmet’in şişedeki su yüksekliği, silindirin içinde 7.5 cm olacaktır. Bu durumda, doğru cevap şıklarda bulunmamaktadır. Ancak silindirin yüksekliğini bulmak için daha fazla ayrıntı verilmesi gerekir.

@Havva_Diken