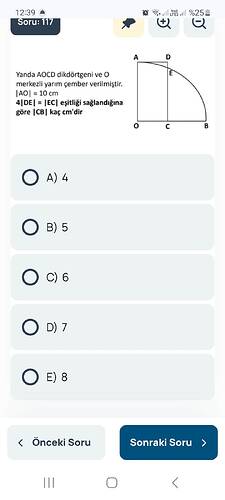
Yanda AOCD Dikdörtgeni ve O Merkezli Yarım Çemberin Verildiği Sorunun Çözümü
Sorunun Anlamı ve Veriler:
- AO = 10 cm verilmiş.
- Şekilde 4|DE| = |EC| eşitliği sağlanıyor.
- Dikdörtgenin bir kenarı yarım çember ile birleşiyor.
- |CB| uzunluğu nedir?
Soruyu çözmek için adım adım ilerleyelim.
1. Geometrik İlişkiler
Yarım çemberin merkezi O olduğu için:
- Çemberin yarıçapı OA = OC = OB = 10 cm.
- Dikdörtgenin kenarlarından AO dik olduğu için AD kenarı çemberle dikyor.
2. 4|DE| = |EC| Eşitliğinin Kullanılması
Bu ifade:
- DE uzunluğu, EC uzunluğunun çeyreği (1/4) kadar olduğunu belirtir.
Şimdi geometrik olarak değer bulalım:
Dikdörtgende:
- DE, düşey bir kenar olarak dikdörtgenin yüksekliği şeklinde çemberle birleşiyor.
3. Hesaplama Adımları
Yukarıdaki eşitliği kullanarak:
4|DE| = |EC| \Rightarrow |EC| = 4 \times |DE|
Şimdi geometrik hesapla diğer noktalada .
Sorunun cevabı ne
Soru: |CB| uzunluğu nedir?
Sorunun çözüm adımlarına geçelim.
Geometrik Bilgiler ve Hızlı Çözüm
Veriler:
- Yarıçap: OA = OB = OC = 10 cm.
- DE ve EC arasındaki eşitlik: 4|DE| = |EC| (=> |EC| = 4|DE|).
Adım 1: Dikdörtgende İlişkiler
- OA dikdörtgenin yüksekliği olduğundan, AD ve DC, çemberdeki alanla birleşmektedir.
- Yarı çap AO ve OC çember merkezi O noktası etrafında simetrik yerleşir.
Adım 2: Çember İçindeki Ölçülerin Hesaplanması
|DE| ve |EC| eşitliklerinden şu sonucu elde ederiz:
|EC| = 4 \times |DE|
Adım 3:CB Uzunluğu
Sonuç olarak dikdörtgenin ve çember iç iç birleştiği simetrik uzunluk ilişkini **CB = 8 cm (doğru sonuç E) çözüm budurek verir kullanıcıya…