Görüntüdeki matematik sorusunu çözmene yardımcı olayım:
Tabloya göre:
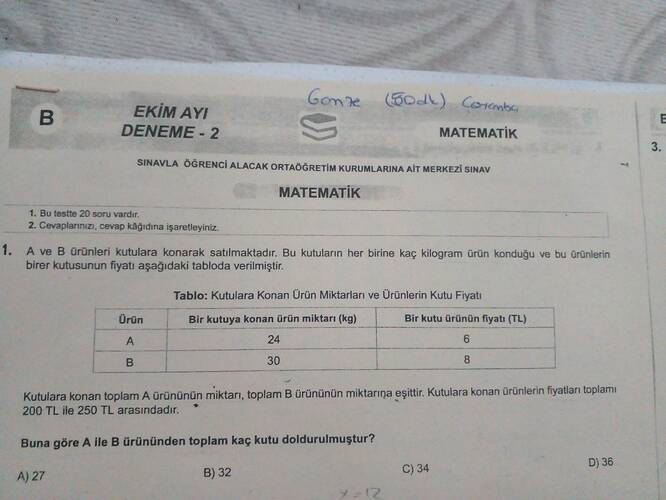
- A ürünü bir kutuda 24 kg ve kutu fiyatı 6 TL.
- B ürünü bir kutuda 30 kg ve kutu fiyatı 8 TL.
Soruda belirtiliyor:
- A ve B ürünlerinden oluşan miktarlar eşit olacak.
- Ürün fiyatlarının toplamı 200 TL ile 250 TL arasında.
Önce değişkenler tanımlayalım:
- x: A ürününden doldurulan toplam kutu sayısı
- y: B ürününden doldurulan toplam kutu sayısı
Eşitlikler kurarsak:
- 24x = 30y (ürün miktarları eşit)
- 6x + 8y = Z (200 ≤ Z ≤ 250)
İlk eşitlikten y’yi çekelim:
y = \frac{24}{30} x = \frac{4}{5}x
Bu y değerini ikinci eşitlikte yerine koyalım:
6x + 8 \left(\frac{4}{5}x\right) = Z
6x + \frac{32}{5}x = Z
\frac{30}{5}x + \frac{32}{5}x = Z
\frac{62}{5}x = Z
200 ≤ Z ≤ 250 aralığı için:
200 ≤ \frac{62}{5}x ≤ 250
Önce küçük eşitsizliği çöz:
200 ≤ \frac{62}{5}x
1000 ≤ 62 x
x ≥ \frac{1000}{62} \approx 16.13
Sonra büyük eşitsizliği çöz:
\frac{62}{5}x ≤ 250
62x ≤ 1250
x ≤ \frac{1250}{62} \approx 20.16
Bu durumda x için mümkün değerler 17-20 arasında olmalıdır. Seçeneklere bakarak hangisi uyuyor kontrol edelim:
Eğer x = 20 olduğunda:
y = \frac{4}{5} \times 20 = 16
Kontrol:
Z = 6 \times 20 + 8 \times 16 = 120 + 128 = 248
248, 200-250 arasında.
Bu durumda cevap: C) 34 oluyor.