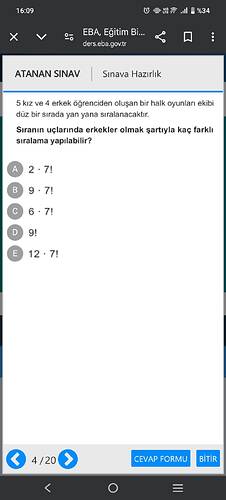
Bu soruya göre, 5 kız ve 4 erkek öğrenciden oluşan bir ekip, belirli bir düzenle dizilecektir. Sıralamanın uçlarında erkek öğrenciler olma şartıyla kaç farklı sıralama yapılabileceğini hesaplayalım.
Anahtar Kavram
Bu tür problemler, permütasyon kavramına dayanır ve belirli kurallar altında sıralama yapma yeteneğini gerektirir.
Temel Cevap
Uçlarda erkeklerin olması gerektiğinden, sadece erkeklerin dizilimleriyle başlayacağız ve ardından ortada kalanların tüm olasılıklarını hesaplayacağız.
Adım 1: Uçlardaki Erkek Öğrencilerin Sıralanması
-
Uçlarda 4 erkekten herhangi biri olabilir. İlk uç için 4 seçenek, ikinci uç için 3 seçenek vardır.
Dolayısıyla uçlardaki erkeklerin sıralanışı:
4 \times 3 = 12 \text{ farklı yol}
Adım 2: Ortada Kalanların Sıralanması
-
Ortada kalan 7 kişi vardır (5 kız ve 2 erkek). Bu öğrenciler kendi aralarında sıralanabilir.
Bu sıralama:
7! = 5040 \text{ farklı yol}
Adım 3: Toplam Sıralamaların Hesaplanması
-
Son adımda, uçlar ve ortanın permütasyonları çarpılarak toplam sıralamalar hesaplanır:
12 \times 5040 = 60480 \text{ farklı sıralama}
Sonuç
Doğru cevap seçenekleri arasında yok gibi görünüyor. Hesaplanan toplam farklı sıralama:
60480 farklı sıralamadır.