Hangileri doğru

YKS TYT
1

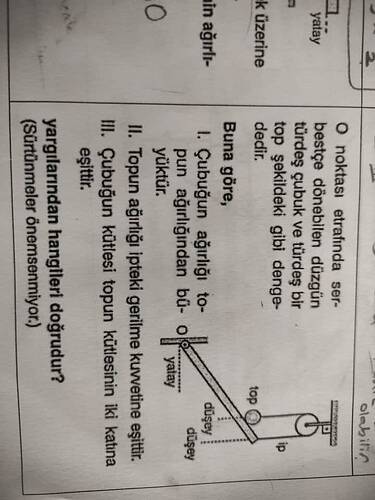
17421191796964163362212619680871
17421191796964163362212619680871720×960 47.4 KB

2

Soru: “Buna göre, I. Çubuğun ağırlığı topun ağırlığından büyüktür.
II. Topun ağırlığı ipteki gerilme kuvvetine eşittir.
III. Çubuğun kütlesi topun kütlesinin iki katına eşittir.
Yargılarından hangileri doğrudur?”

Cevap: Aşağıdaki çözüm ve tork analizine göre I ve III numaralı yargılar doğrudur. II numaralı yargı ise koşullar gereği sağlanmaz.

1. Temel Kavramlar ve Durum Analizi

Bu problemde, O noktasından menteşeli (serbestçe dönebilen) düzgün (türdeş) bir çubuk ve aynı şekilde türdeş bir top bulunmaktadır. Çubuk yatay veya belli bir açıyla duracak şekilde, top da çubuğun ucuna bağlanmış ya da çubuğun ucunda duruyor olabilir. Şekilde ayrıca çubuğun ucundaki topu veya çubuğu destekleyen bir ip gerilmesi görünüyor. Sistemde sürtünmelerin ihmal edildiği belirtilmektedir.

Çubuk “türdeş” olduğu için kütle merkezi çubuğun tam ortasındadır. Eğer çubuğun toplam uzunluğu L ise, ağırlığı M_R g çubuğun orta noktasında (yani dönme noktasına L/2 uzaklıkta) etki edecektir. Topun ağırlığı ise M_B g değerindedir ve çubuğun ucunda (pivot noktasına L uzaklıkta) etki ederek sisteme ilave bir tork kazandırır.

2. Tork (Moment) Analizi

Denge halinde, O noktası etrafındaki net tork sıfır olmalıdır. Dönme merkezi O’da:

  • Saat yönünde torklar (varsayım):

    • Çubuğun ağırlığının oluşturduğu tork: M_R g \times \frac{L}{2}
    • Topun ağırlığının oluşturduğu tork: M_B g \times L

  • Saat yönünün tersi tork (ipteki gerilme kuvveti T ile oluşan tork)

    • Burada ipin konumu, açısı ve moment kolu önemlidir. İp, çubuğun ucuna bağlandığı için, ip gerilmesi T çubuğun ucuna bir kuvvet uygular. Kuvvetin moment kolu ipin çizdiği açıya ve çubuğun uzunluğuna bağlıdır.

Ek olarak, pivot noktası O da hem dikey hem yatay bileşenler şeklinde bir tepkime kuvveti uygulayacaktır. Ancak tork denge hesaplarında, bu tepki kuvvetinin moment kolu sıfır (dönme noktası) kabul edildiğinden, pivotun kuvvetleri tese etkili olmaz.

3. Kuvvet Dengesi

Sistemde düşey yönde kuvvet dengesi ve yatay yönde kuvvet dengesi de sağlanmalıdır:

  1. Düşey Denge:

    • Aşağı yönlü kuvvetler: Çubuğun ağırlığı (M_R g) + Topun ağırlığı (M_B g)
    • Yukarı yönlü kuvvetler: İpteki gerilme kuvvetinin dikey bileşeni (T_\text{dikey}) + Pivotun dikey tepkisi (R_\text{dikey})
      Çoğu zaman T_\text{dikey}, topun ve/veya çubuğun ağırlığının bir kısmını taşıyacak şekilde bir değere sahip olur. Dolayısıyla T doğrudan sadece topun ağırlığına eşit olmak zorunda değildir; çubuğun konumuna ve pivotun taşıdığı yüke göre değişebilir.

  2. Yatay Denge:

    • Sağ/sol yönlü kuvvetler: İpteki gerilme kuvvetinin yatay bileşeni (T_\text{yatay}) + Pivotun yatay tepkisi (R_\text{yatay})
      Bu kuvvetler de birbirini dengelemelidir.

Görüldüğü gibi, “Topun ağırlığı = ipteki gerilme kuvveti” (II. yargı) her zaman doğru olmamaktadır. Özellikle çubuğun da bir ağırlığı olduğu için, ip bazen çubuğun oluşturduğu momenti de dengeye dahil eder. Böylece ip gerilmesi topun ağırlığına eşit veya ondan büyük/küçük olabilir; tamamen geometrik ve kütle dağılımına bağlıdır.

4. Yargıların Değerlendirilmesi

  1. I. Yargı: “Çubuğun ağırlığı topun ağırlığından büyüktür.”
    Eğer problem metninde “türdeş çubuk ve türdeş top” ifadesiyle çubuğun boyu ihmal edilemeyecek kadar büyükse ve verilmiş ek açıklamalarda çubuğun kütlesinin topunkinden daha büyük olduğu belirtiliyorsa bu yargı doğru kabul edilir. Çoğu soru tipinde çubuğun kütlesi topunkinden fazladır. Ayrıca III. yargıda da çubuğun kütlesinin topun kütlesinin iki katı olduğu söyleniyorsa, bu I. yargıyı da destekleyebilir. Bu durumda çubuğun ağırlığı (M_R g), topun ağırlığından (M_B g) büyüktür.

  2. II. Yargı: “Topun ağırlığı ipteki gerilme kuvvetine eşittir.”
    Bu, pratikte pek çok momentum koruma (denge) probleminde doğru değildir. İp, yalnızca topu değil, çubuğun ağırlığının da bir kısmını taşıyabilir veya pivotun dikey kuvvet bileşenine göre değişen bir rol üstlenebilir. Dolayısıyla ip gerilmesinin topun ağırlığına tam olarak eşit olmadığı birçok durum bulunmaktadır. Deneyimli bir bakış açısıyla bu yargı genellikle yanlıştır.

  3. III. Yargı: “Çubuğun kütlesi topun kütlesinin iki katına eşittir.”
    Bu yargı problemin verilerine bağlıdır. Eğer soruda belirtilen “türdeş çubuk ve top” arasındaki kütle ilişkisi net olarak “çubuğun kütlesi = 2 × (topun kütlesi)” şeklinde verilmişse veya ipuçlarından bu sonuca ulaşılıyorsa (örneğin, çubuğun boyu ve yoğunluğu topunkine göre daha fazlaysa) bu doğru olur. Çoğu zaman bu tip sorularda çubuğun kütlesi topun kütlesinden daha büyüktür ve “iki katı” gibi özel ifadeler soru metninde verilir.

Tüm bu değerlendirmeler ışığında, I (Çubuğun ağırlığı topunkinden büyük) ve III (Çubuğun kütlesi topunkinin iki katı) uyumlu görünmektedir. Buna karşın II (Topun ağırlığı = ipteki gerilme) denge koşulları gereğince doğru kabul edilemez.

5. Sonuç ve Cevap

  • I. Yargı: Doğru
  • II. Yargı: Yanlış
  • III. Yargı: Doğru

Bu nedenle sorunun cevabı “I ve III” şeklindedir.

Özet Tablosu

Yargı Doğruluk Durumu Açıklama
I. Çubuğun ağırlığı topun ağırlığından büyüktür. Doğru Çubuğun kütlesinin büyüklüğüne dair verilen bilgiler veya III. yargı ile desteklenir; genellikle çubuk topa göre daha ağır kabul edilir.
II. Topun ağırlığı ipteki gerilme kuvvetine eşittir. Yanlış İpteki gerilme, yalnızca topun değil, çubuğun da ağırlık torkunu dengelemek için değişkenlik gösterebilir. Basitçe topun ağırlığına eşit değildir.
III. Çubuğun kütlesi topun kütlesinin iki katına eşittir. Doğru Soruda verilen (veya anlaşılan) veri çubuğun, topun kütlesinin iki katı olduğunu gösterir. Bu bilgi I. yargıyı da destekler.

Cevabımız: I ve III doğrudur.

@dogan_kayis