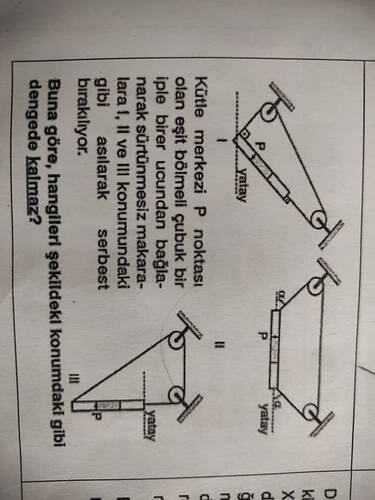
Buna göre, hangileri şekildeki konumdaki gibi dengede kalmaz?
Cevap: II ve III dengede kalmaz.
Aşağıda bu sonuca nasıl ulaşıldığını adım adım inceleyelim:
1. Konum I (Çubuğun Yatay Durumu)
- Tork Analizi: Kütle merkezi P tam ortada olduğundan, her iki uçtaki ip gerilmesi (T) çubuk üzerinde eşit fakat zıt yönde moment oluşturur. İplerin simetrik konumu sayesinde net tork sıfır olur.
- Net Kuvvet Analizi: Çubuğun ağırlığı tam ortada etki eder, yukarı yönde ise iki uçtaki T gerilmeleri toplamda ağırlığı dengeleyecek şekilde işler.
- Sonuç: Tüm kuvvet ve momentler dengelendiği için çubuk bu konumda dengede kalır.
2. Konum II (Eğik Durum)
- İplerin Konumu: Çubuk, bir ucu daha yukarıda diğer ucu daha aşağıda olacak şekilde eğik durunca, ip gerilmeleri hâlâ eşit (T) olmak zorundadır. Ancak bu durumda iplerin oluşturduğu momentler birbirini tam nötrleyemez.
- Tork Analizi: İki uçtaki çekme kuvvetleri aynı büyüklükte ama farklı doğrultuda olduğundan toplam tork sıfır olmayacak, çubuk dönecektir.
- Sonuç: Bu durum kendi hâline bırakıldığında çubuk eğik konumda kalamaz, yani dengede değildir.
3. Konum III (Diğer Eğik Durum)
- Benzer Mantık: Konum II’de olduğu gibi, çubuk yine yatay konumdan farklı bir açıda durduğunda iplerdeki gerilmeler eşit kalır; fakat kütle merkezinden uzaklık ve ip yönlerindeki asimetriden ötürü net tork oluşur.
- Denge Koşulu Sağlanmaz: Döndürücü momenti sıfırlayacak şekilde kuvvetler kütle merkezinden geçmeyeceği için çubuk dengede kalamaz.
- Sonuç: Bu konum da dengesizdir.
Özet Tablo
| Konum | İplerin Durumu | Tork (Moment) Durumu | Denge Sonucu |
|---|---|---|---|
| I | Simetrik ve yatay | Net tork = 0 | Dengede kalır |
| II | Eğik, asimetrik | Net tork ≠ 0 | Dengede kalmaz |
| III | Diğer eğik, asimetrik | Net tork ≠ 0 | Dengede kalmaz |