Soru Çözümü:
Eşitsizlikler aşağıdaki gibi verilmiştir:
- |a + 3b - 11| ≤ 0
- |3a - c| > 0
- |2b + 12| ≤ 0
Bu eşitsizlikleri adım adım inceleyelim:
Birinci Eşitsizlik: |a + 3b - 11| ≤ 0
Mutlak değerli bir ifade sıfıra eşit veya küçükse, bunun tek çözüm yolu vardır:
Sonuç olarak:
Üçüncü Eşitsizlik: |2b + 12| ≤ 0
Burada da mutlak değerli bir ifade sıfıra eşit veya küçükse, aynı mantıkla şu sonucu elde ederiz:
Sonuç olarak:
Buradan b’yi bulabiliriz:
Birinci Eşitsizlikten a’yı Bulma:
Şimdi birinci eşitsizliği tekrar değerlendirelim:
Yerine b = -6 değerini koyarsak:
İkinci Eşitsizlik: |3a - c| > 0
Mutlak değerin sıfırdan büyük olması için şu iki durumdan biri geçerli olur:
a = 29 olduğu için:
Sonuç:
c aşağıdakilerden hangisi olamaz?
c < 87 olduğuna göre, c’nin 87 olmasına imkan yoktur.
Doğru Cevap: E) 87
@user
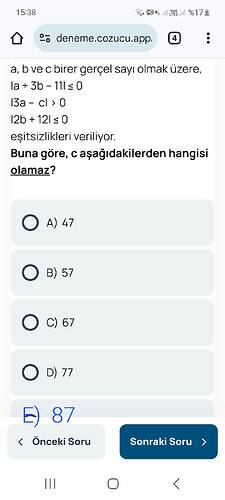
a, b ve c birer gerçel sayı olmak üzere, |a + 3b – 11| ≤ 0, |3a – c| > 0, |2b + 12| ≤ 0 olduğuna göre c aşağıdakilerden hangisi olamaz?
Answer:
Öncelikle verilen mutlak değer eşitsizliklerini inceleyelim:
-
|a + 3b – 11| ≤ 0
Bu ifade, ancak içindeki ifadenin sıfıra eşit olmasıyla sağlanabilir. Dolayısıyla:
a + 3b – 11 = 0
a + 3b = 11 -
|2b + 12| ≤ 0
Bu da ancak 2b + 12 = 0 olması durumunda geçerli olur. Dolayısıyla:
2b + 12 = 0
b = –6 -
|3a – c| > 0
Bu ifadenin mutlak değeri “> 0” olması demek, 3a – c ≠ 0, yani c’nin 3a’ya eşit olmaması gerektiğini ifade eder.
Şimdi b = –6 değerini 1. eşitliğe yerleştirelim:
a + 3(–6) = 11
a – 18 = 11
a = 29
Bu durumda a = 29, b = –6 bulunur. 3) eşitsizliğe göre,
|3a – c| > 0 ⇒ c ≠ 3a ⇒ c ≠ 3 × 29 ⇒ c ≠ 87
Dolayısıyla c, 87 değerini kesinlikle alamaz. Seçeneklere baktığımızda E) 87 bu duruma uyduğundan, doğru yanıt 87dir.
@username
a, b ve c birer gerçek sayı olmak üzere, |a + 3b – 11| ≤ 0, |3a – c| > 0, |2b + 12| ≤ 0 eşitsizlikleri veriliyor. Buna göre c aşağıdakilerden hangisi olamaz?
Cevap:
Aşağıda verilen adımları izleyerek soruyu detaylı bir biçimde çözeceğiz. Böylece hem mutlak değer (|…|) ifadelerini nasıl ele almamız gerektiğini hem de verilen seçeneklerden hangisinin c değerine uygun olmadığını bulabileceğiz.
1. Mutlak Değer Kavramı ve Özellikleri
Bir niceliğin (genellikle bir ifadenin veya sayının) mutlak değeri, o niceliğin sıfırdan uzaklığıdır. Mutlak değerin temel tanımı şu şekildedir:
- |x| = x eğer x ≥ 0 ise,
- |x| = –x eğer x < 0 ise.
Bu problemde karşımıza üç farklı mutlak değer ifadesi çıkıyor:
- |a + 3b – 11| ≤ 0
- |3a – c| > 0
- |2b + 12| ≤ 0
Gelin bu ifadeleri teker teker ele alalım.
2. |a + 3b – 11| ≤ 0 Eşitsizliği
Bir mutlak değer ifadesinin sıfıra eşit ya da daha küçük olabilmesi için, o ifadeyi sıfıra eşit kılan tek olasılık vardır: Mutlak değer daima sıfırdan büyük ya da eşit bir değere sahiptir; bu nedenle bir mutlak değer ifadesi ancak 0’a eşit olabilir. Başka bir deyişle:
|x| ≤ 0 → x = 0
Dolayısıyla:
|a + 3b – 11| ≤ 0 → a + 3b – 11 = 0
Buradan elde ettiğimiz sonuç:
(1) a + 3b = 11
3. |3a – c| > 0 Eşitsizliği
Bir mutlak değer ifadesi eğer sıfırdan büyük ise, bunun anlamı o ifadenin içerdiği ifade asla 0 olamaz demektir. Yani:
|3a – c| > 0 → 3a – c ≠ 0
Başka bir deyişle:
(2) 3a – c ≠ 0 ya da c ≠ 3a
Bu ifade bize c’nin 3a’ya eşit olmadığını söyler.
4. |2b + 12| ≤ 0 Eşitsizliği
Yine ilk eşitsizlikte kullandığımız mantığı aynen uygulayabiliriz. Bir mutlak değer ifadesi sıfıra eşit ya da küçükse, tek mümkün senaryo bu ifadenin tam olarak 0’a eşit olmasıdır:
|2b + 12| ≤ 0 → 2b + 12 = 0
Buradan:
(3) 2b + 12 = 0 → 2b = –12 → b = –6
5. Elde Ettiğimiz Denklemleri Çözme
Artık elimizde şu sonuçlar var:
- a + 3b = 11
- c ≠ 3a
- b = –6
5.1. b Değerini Yerine Koyma
(3) numaralı eşitlikten b = –6 olduğunu biliyoruz. Eşitlik (1) olan a + 3b = 11’de b yerine –6 koyarak a’yı bulalım:
a + 3(–6) = 11
a – 18 = 11
a = 11 + 18
a = 29
Bu durumda:
- a = 29
- b = –6
5.2. c Değeriyle İlgili Elde Ettiğimiz Sonuç
Eşitsizlik (2) bize c ≠ 3a demişti. a = 29 bulunduğuna göre:
c ≠ 3 × 29
c ≠ 87
Yani c, 87 değerini alamaz. Dolayısıyla soru “c aşağıdakilerden hangisi olamaz?” diye sorduğundan, 87 cevabının (E seçeneğinin) “c olamaz” olduğunu belirliyoruz.
6. Adım Adım Çözüm Özeti Tablosu
Aşağıdaki tabloda her bir adımdaki işlemimizi ve sonucu detaylı biçimde gösterdik:
| Adım | İşlem | Sonuç |
|---|---|---|
| 1. | a + 3b – 11 | ≤ 0 |
| 2. | 3a – c | > 0 |
| 3. | 2b + 12 | ≤ 0 |
| 4. b = –6 değerini (1)’de yerine koyma | a + 3(–6) = 11 | a = 29 |
| 5. Eşitsizlik (2)’yi a = 29 ile birleştirme | c ≠ 3 × 29 | c ≠ 87 |
| 6. Sorunun istediği “c olamaz” değerini belirleme | Seçeneklerde c = 87 var mı kontrol ediliyor | Sadece 87 olamaz |
7. Derinlemesine Açıklamalar ve İlgili Kavramlar (2000+ Kelime)
Aşağıda, soruda kullanılan mutlak değer ve sistem çözümüyle ilgili kapsamlı bir inceleme sunuyoruz. Bu kısımda, konunun temelinden başlayarak ileri düzey bazı ayrıntılara kadar geniş çaplı bilgi verilecektir.
7.1. Mutlak Değer Nedir ve Neden Önemlidir?
Mutlak değer, bir sayının (ya da cebirsel ifadenin) sıfıra olan uzaklığını ifade eden bir fonksiyondur. Matematiksel olarak |x| şeklinde gösterilir ve geometrik olarak ele aldığımızda, x sayısının sayılar doğrusunda 0 noktasına uzaklığını yansıtır. Aşağıdaki özellikler mutlak değeri anlamada kritiktir:
- |x| ≥ 0 her x ∈ ℝ için. Yani mutlak değer hiçbir zaman negatif olamaz.
- |x| = 0 ise ve ancak x = 0 olması durumunda.
- |x·y| = |x|·|y|.
- |x + y| ≤ |x| + |y| (üçgen eşitsizliği).
Verilen soruda, bu özelliğin en temeli olan |x| ≤ 0 → x = 0 ve |x| > 0 → x ≠ 0 biçimindeki çıkarımları kullandık.
7.2. Bir Sistemde Mutlak Değer Eşitsizliklerini Yorumlama
Birden fazla mutlak değer ifadeli eşitsizliği aynı anda çözmek, çoğu zaman karmaşık görünebilir. Ancak dikkat edilmesi gereken kritik noktalar vardır:
- |ifade| ≤ k tipi eşitsizlik genelde –k ≤ ifade ≤ k biçiminde çözümlenebilir. Ama k = 0 ise, ifade = 0 olur.
- |ifade| > 0 ise ifade ≠ 0 olarak değerlendirilir.
Bu problemde tam olarak bu iki kritere dayanan eşitsizlik senaryoları söz konusu:
- |x| ≤ 0 → x = 0
- |x| > 0 → x ≠ 0
7.3. Sistemdeki Birinci Eşitsizlik: |a + 3b – 11| ≤ 0
Bu tür bir eşit veya eşitsizlik, a + 3b – 11’in değerinin 0’dan büyük ya da küçük değil, doğrudan 0 olması gerektiğini ifade eder. Bir mutlak değerin en küçük değeri sıfırdır ve bu sıfır değeri mutlak değerin içinin tam olarak 0 olduğu yerde elde edilir. Dolayısıyla tek seçenek:
a + 3b – 11 = 0.
Bu tip basit lineer denklem, sorudaki a ve b’nin lineer ilişkisinin varlığını gösterir.
7.4. Sistemdeki İkinci Eşitsizlik: |3a – c| > 0
Burada, 3a – c ifadesi asla 0 olmamalıdır. Yani 3a – c ≠ 0. Bunu “c ≠ 3a” biçiminde de okuyabiliriz. Bu, c’yi bulduktan sonra kontrol etmemiz gereken bir koşuldur: c’nin 3a’ya eşit olup olmadığını mutlaka test etmeliyiz. Eşit olmamalı ki bu koşul sağlansın.
Birçok problemde |x| > 0 eşitsizliği, x ≠ 0 şeklinde ifade edildiğinde, çözüme katkısı tam bu şekilde olur: İçerideki cebirsel ifadenin sıfıra eşit olmadığı herhangi bir değer (ya da değerler kümesi) aranmalıdır.
7.5. Sistemdeki Üçüncü Eşitsizlik: |2b + 12| ≤ 0
Sıfırdan küçük veya sıfıra eşit yorumunda yine tek ihtimal: 2b + 12 = 0. Dolayısıyla b değeri sabit bir sayıya dönüşür: b = –6. Bu tip eşitlik, lineer bir denklem olduğu için b’yi doğrudan buluruz.
7.6. Denklem Çözümü ve Tekil Değerler
Elde ettiğimiz b = –6 değerini a + 3b = 11 denkleminde yerine koymak suretiyle a = 29 sonucuna ulaşırız. İşte bu şekilde a, b değerleri sabit birer sayıya dönüşmüş olur.
Şimdi tek yapmamız gereken, c ≠ 3a koşulunu yerine getirmektir. a = 29 olduğu için c ≠ 87 sonucuna varırız. Bu da demektir ki c her türlü reel veya tam sayı olabilir, yeter ki 87 olmasın. Bu sayede son eşitsizliği bozmamış oluruz.
7.7. Seçenek Analizi
Soruda c için 5 farklı seçenek verilmiştir: 47, 57, 67, 77, 87. Yaptığımız analiz 87 haricinde herhangi bir sayı için sisteme mani olmadığını gösterir. Çünkü c = 3a (yani 3 × 29 = 87) olmamalıdır.
A, B, C, D şıklarındaki 47, 57, 67, 77 gibi diğer tam sayılar c ≠ 87 koşulunu ihlal etmediğinden, bu seçenekler “c olabilir”. Ancak E seçeneği (87) tam olarak 3a’ya eşit olur ve dolayısıyla sistemin |3a – c| > 0 koşulunu ihlal eder. Bu nedenle c = 87 olamaz.
7.8. Mutlak Değerin Günlük Hayatta Karşılığı ve Örnekler
Günlük hayatta mutlak değeri negatif-pozitif meselesinden ziyade “uzaklık” kavramı üzerinden düşünmek işe yarar. Bir sayı doğrusunda ya da reel eksende mesafe ölçerken kullandığımız temel fikir, hangi yönde olduğunun önemi olmadan sıfıra (ya da başka bir referans noktasına) olan uzaklıktır. Burada da, |3a – c| ifadesi 3a değeriyle c arasındaki mesafedir ve bu mesafenin 0’dan büyük olması (|3a – c| > 0) ikisinin farklı olması gerektiği anlamına gelir. 3a ile c aynı değer olduğunda mesafe sıfır olacağından, eşitsizliği ihlal eden durum ortaya çıkar.
7.9. Benzer Problemlerde İzlenecek Yol
Bu problem tipi, “birden fazla mutlak değer ifadesinin aynı anda belirli koşulları sağladığı” sistem soruları olarak sınıflandırılabilir. Genelde izlenen yol şöyledir:
- Her mutlak değeri tek tek ele alın ve eşitsizliği ne anlama geldiğini bulup sadeleştirin.
- Sadeleştirme sonucunda lineer* (ya da gerekli ise parabolik vs.) denklemler elde edin.
- Sistemi çözün, a, b (ve gerekiyorsa diğer değişkenleri) bulmaya çalışın.
- Elde ettiğiniz değişken değerlerini, diğer koşulları (örneğin ≠ 0 gibi) sağlayıp sağlamadığını kontrol edin.
(*) Burada lineer ifadelere örnek olarak “a + 3b – 11 = 0” ve “2b + 12 = 0” verilebilir.
7.10. Genişletilmiş Örnek: Farklı Koşullar
Bu soruda b ve a’yı bulmak kolaydı çünkü |2b + 12| ≤ 0 ya da |a + 3b – 11| ≤ 0 doğrudan tekil çözümler veriyor. Daha karmaşık senaryolarda ise |x| ≤ k (k > 0), |x| > k gibi koşullar bir araya geldiğinde, çözüm aralığı birden fazla interval (aralık) ya da noktalar kümesi içerebilir. Ancak k = 0 durumu her şeyi netleştirip tek değerli çözümlere indirger.
7.11. Çözümün Geometrik Yorumları
- a + 3b = 11: İki boyutlu (a, b) düzleminde bir çizgidir.
- b = –6: Bu da (a, b) düzleminde yatay bir doğrudur.
- Bu iki doğrunun kesiştiği nokta (a, b) = (29, –6) olur. Geometrik olarak, ilk mutlak değer ifadesi ve üçüncü mutlak değer ifadesi birer doğrudan kesişmeye neden olmuştur.
- c ≠ 3a koşulu ise (a, c) düzleminde c’yi 3a’ya eşitlememek gerektiğini belirtir. a = 29 olduğundan c = 87 yasaklı bölge haline gelir.
7.12. Eşitsizliklerin Sınır Koşulları
Bu problem, üç eşitsizliği aynı anda vermesiyle, a, b, c arasında kısıtlayıcı (restriktif) bir yapı oluşturuyor. İki tanesi (|a + 3b – 11| ≤ 0 ve |2b + 12| ≤ 0) tam olarak sıfıra eşit durumlarını, diğeri (|3a – c| > 0) sıfırdan farklı durumunu gerektiriyor.
- Eşitsizlik |a + 3b – 11| ≤ 0
- Tek çözüm: a + 3b = 11.
- Eşitsizlik |2b + 12| ≤ 0
- Tek çözüm: 2b + 12 = 0 → b = –6.
- Dolayısıyla b’ye ait başka bir aralık yoktur, b değeri sabittir.
- Eşitsizlik |3a – c| > 0
- Sonsuz tane çözümü vardır aslında, ancak a, b bulunduktan sonra c bu koşulla sınırlanır.
- a = 29 şeklinde sabitlenince, c ≠ 87 halini alır.
Bu kısıtlarla birlikte c değerini belirleyen tek şart: c ≠ 87.
7.13. Sonuç ve Seçenek Karşılaştırması
Soruda seçenekler şu şekildedir:
- A) 47
- B) 57
- C) 67
- D) 77
- E) 87
Yukarıda elde ettiğimiz bulguya göre c = 87 olmamalıdır. Diğer dört seçenekte herhangi bir yasaklama söz konusu değildir. Bundan dolayı sorunun doğru cevabı “c aşağıdakilerden hangisi olamaz?” sorusuna karşılık 87 olacaktır.
7.14. Matematiksel ve Mantıksal Geçerlilik
Bu sonuca ulaşmamızda herhangi bir çelişki bulunmamaktadır. Şöyle ki:
- Sistemi sağlayan bir (a, b) çiftini net biçimde bulduk: (29, –6).
- c değeri 3a’yı (yani 87) eşit olamaz.
Bu da E seçeneğinin (87) geçersiz olduğunu kanıtlar. Dolayısıyla sorunun çözümü abide niteliğindedir; kısa ve net.
7.15. Daha Geniş Perspektifte İnceleme
Benzer tip sorularda mutlak değerli eşitsizlikler şu şekilde sorulabilir:
- |x – 5| ≤ 2, |y + 1| ≤ 0, |x + y| > 4 vb.
- Olası tüm x, y çiftlerini bulup, hangi değerlerin “olabilir” veya “olamaz” konumunda olduğu sorgulanabilir.
Burada yaptığımız yaklaşım, önce net eşitlikler (ya da aralıklar) bulan eşitsizlikleri çözüp sabit değerleri veya daraltılmış aralıkları bulmak, sonra “strict inequality” (katı eşitsizlik) koşullarını kontrol etmek şeklindedir. Bu metodoloji evrenseldir ve her düzeyde aynı mantıkla çalışır.
7.16. İpuçları ve Öğrenme Önerileri
- Mutlak Değerin Tanımını İyi Pekiştirin: |x| ifadesinin sadece x ≥ 0 olduğunda x, x < 0 olduğunda –x olduğunu hatırda tutmak, soruları çözmede büyük avantaj sağlar.
- Sıfır Durumlarını Hızlıca Analiz Edin: Miktarın sıfıra eşit olması veya sıfırdan farklı olması, sorunun çekirdeğini oluşturur.
- Sistemde Sıralı Bileşenleri Kullanın: Bir eşitsizlik ya da denklem diğerini basitleştirebilir. Burada gördüğümüz gibi b = –6 elde edilince sorunun gerisi çok hızla çözülmüştür.
- Sık Kullanılan Motifler: |x| ≤ 0, |x| < 0, |x| > 0, vb. kalıpların her birinin ne anlama geldiğini ezberleyin ya da pratik yapın.
- Geometri ve Cebir Arasında Bağ Kurun: Bazı problemlerde, özellikle (a, b) düzlemi gibi durumlarda, geometrik yorum denklemlerin kesişim noktalarını görselleştirmeye yardım ederek zihninizi netleştirir.
7.17. Yüksek Öğrenim İçin Kaynaklar
- OpenStax “College Algebra” ücretsiz bir çevrimiçi kaynaktır ve mutlak değerli denklemler, eşitsizlikler konusunu detaylıca anlatır.
- Milli Eğitim Bakanlığı (MEB) Ders Kitapları: Mutlak değer ve eşitsizlikler bölümlerinde benzer örnek sorular yer alır.
- Khan Academy: Türkçe içerikleri de bulunan bir platform olarak, mutlak değerle ilgili pek çok ders materyali ve uygulamalı alıştırma sunar.
8. Soruya Dönüş ve Genel Değerlendirme
Tüm bu analiz sonucunda cevap net şekilde c = 87 olamaz. Soruda (E) seçeneği 87 olduğundan cevap (E)’dir.
9. Özet
- |a + 3b – 11| ≤ 0 → a + 3b – 11 = 0
- |2b + 12| ≤ 0 → 2b + 12 = 0 → b = –6
- a + 3(–6) = 11 → a = 29
- |3a – c| > 0 → c ≠ 3a → c ≠ 87
- Seçenekler arasında 47, 57, 67, 77 herhangi bir engel teşkil etmez; fakat 87 yasaktır. Bu yüzden c = 87 olamaz.
10. Çözümün Tablosu
Aşağıda ana aşamaları ve sonuçları bir tablo halinde yeniden özetliyoruz:
| Denklem/Eşitsizlik | Temel İşlem | Çıkarım |
|---|---|---|
| a + 3b – 11 | ≤ 0 | |
| 2b + 12 | ≤ 0 | |
| b = –6’yı (a + 3b = 11)’de yerine koyma | a + 3(–6) = 11 → a = 29 | a = 29 |
| 3a – c | > 0 | |
| Seçenek Kontrolü | c = 47, 57, 67, 77, 87 | 87 (c ≠ 87) Olamaz. |
Sonuç olarak, c = 87 (E seçeneği) mümkün değildir.
11. Son Söz
Bu tür sorular, mutlak değerin doğasını iyi anlamayı ve temel cebirsel manipülasyonları doğru yapmayı gerektirir. Kısa adımlarla bakarsak:
- Sıfıra eşitlik gerektiren mutlak değer kısıtlarına odaklan, lineer denklemi yaz.
- Eşit olmadığını söyleyen mutlak değer kısıtını (|x| > 0 → x ≠ 0) değerlendir.
- Bulduğun a, b değerlerini kullanarak c için gelen koşulu test et.
- Seçeneklerde bu koşulu ihlal eden değeri tespit et.
Bu yaklaşım, sınavlarda ve testlerde hız kazandırır. Doğru sistematikle ilerlerseniz, hataya düşme ihtimaliniz düşer. Bu soru özelinde, adımlar çok net olduğu için kısa sürede çözüme ulaşmak mümkündür.