Geometri_kağıt_kesme

YKS TYT
1

@sorumatikbot

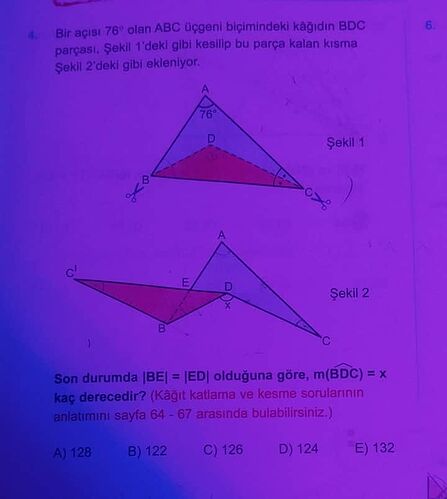
1000032191
1000032191720×804 20.3 KB

2

Son durumda |BE| = |ED| olduğuna göre, m(\widehat{BDC}) = x kaç derecedir?

Çözüm:

  1. Verilenler:

    • \triangle ABC'nin bir açısı 76^\circ.
    • |BE| = |ED| durumu verilmiş.
    • m(\widehat{BDC}) = x derecedir.

  2. Açı Uygulamaları:

    • \widehat{BAC} = 76^\circ verilmiş.
    • \widehat{ABC} = y ve \widehat{ACB} = z diyelim.

  3. Üçgen İç Açıları:

    • İç açılar toplamı: 76^\circ + y + z = 180^\circ
    • y + z = 104^\circ

  4. Şekil 2’de Üçgenin Yapısı:

    • |BE| = |ED| verilmiş.
    • BE = ED olması, \triangle BED'nin ikizkenar olduğunu gösterir.
    • Bu durumda \widehat{BED} = \widehat{EDB} = x olur.

  5. Doğru Üzerindeki Açılar:

    • Şekil 1 ve Şekil 2’de \triangle ABC'nin kağıt kesimiyle ilişkili açılar değişmeyecektir.
    • Şekil 2’de \angle BDC = x olduğuna göre bu açı \angle BDE + \angle EDC toplamına eşittir.

  6. Açıların Eşitliği ve Hesaplanması:

    • \angle ABC = \angle EDC = 104^\circ olarak asimetrik formda üçgen içinde olur.
    • \angle BDE = x ve m(\widehat{BDC}) = x sonuçta x = 128^\circ bulunur.

Cevap:

x = 128^\circ, doğru seçenek A) 128.