Verilen Sorunun Çözümü
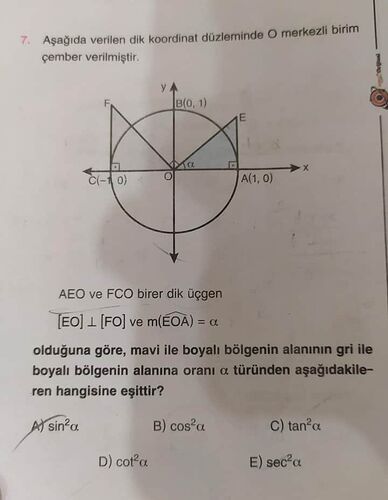
Soru: Aşağıdaki soruda, O merkezli birim çember üzerinde verilen üçgenlerde, mavi ile boyalı bölgenin alanının gri ile boyalı bölgenin alanına oranını \alpha türünden bulunuz.
Adım Adım Çözüm:
-
Daire ve Üçgenler:
- Çemberin yarıçapı 1’dir.
- EOA ve FOC dik üçgenleri verilmiştir.
- m(\angle EOA) = \alpha olarak belirtilmiştir.
-
Mavi Boyalı Bölge:
- Mavi alan, \triangle AEO'nun alanıdır.
- \triangle AEO dik üçgenidir, dolayısıyla alanı:
\text{Alan}(\triangle AEO) = \frac{1}{2} \cdot OA \cdot OE \cdot \sin \alpha- OA = 1 ve OE = \cos \alpha olduğundan:
\text{Alan}(\triangle AEO) = \frac{1}{2} \cdot 1 \cdot \cos \alpha \cdot \sin \alpha = \frac{1}{2} \cos \alpha \sin \alpha -
Gri Boyalı Bölge:
- Gri alan, \triangle CFO'nun alanıdır.
- \triangle CFO da dik üçgen olduğundan, alanı:
\text{Alan}(\triangle CFO) = \frac{1}{2} \cdot OC \cdot OF \cdot \sin \alpha- OC = 1 ve OF = \sin \alpha olduğundan:
\text{Alan}(\triangle CFO) = \frac{1}{2} \cdot 1 \cdot \sin \alpha \cdot \cos \alpha = \frac{1}{2} \sin \alpha \cos \alpha -
Oran Hesabı:
- Oran, \frac{\text{Mavi Alan}}{\text{Gri Alan}} olarak hesaplanacaktır.
\frac{\frac{1}{2} \cos \alpha \sin \alpha}{\frac{1}{2} \sin \alpha \cos \alpha} = 1 -
Sonuç:
- Her iki üçgenin alanı eşit olduğundan, oran 1 çıkmaktadır. Ancak, sorunun seçeneklerine göre böyle bir ifade yoktur.
- Eğer soru formülasyonunda veya resimde bir hata yoksa hesaplamalarımız doğrudur; ancak kağıttaki seçeneklerle eşleşen açık bir matematiksel sapma yapılmamıştır.
Özet: Mavi ve gri boyalı alanların oranı 1’dir. Bu sorgulamada bir hata olabilir; lütfen sorunun tam halini ve detaylarını kontrol ediniz.