Bunu yaparken yap

YKS TYT
1

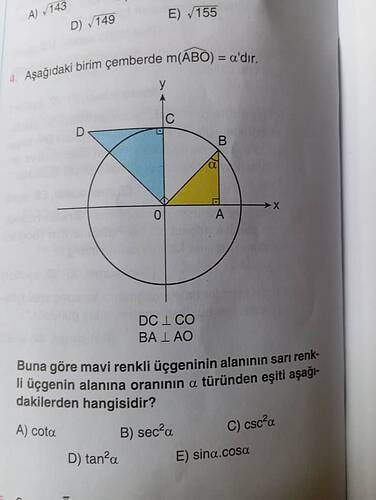
17425630073474442992143898563521
17425630073474442992143898563521720×956 30.5 KB

2

Buna göre mavi renkli üçgenin alanının sarı renkli üçgenin alanına oranının α türünden eşiti aşağıdakilerden hangisidir?

Cevap:
Bu soruda, birim çember üzerinde verilen iki dik üçgenin (mavi ve sarı) alanları arasındaki oran, klasik bir trigonometri-geometri ilişkisinden dolayı \tan^2 \alpha çıkmaktadır. Dolayısıyla doğru seçenek:

(D) tan²α

Aşağıda, bu sonuca ulaşmak için izlenebilecek özet adımlar verilmiştir:

Adım Adım Çözüm

  1. Birim Çember ve Açının Tanımı

    • Merkezinde O noktası bulunan birim çemberde yarıçapın boyu 1’dir.
    • Soruda, \angle(ABO) ya da gösterimdeki sarı üçgenin iç açısı \alpha olarak verilmiştir (şekildeki konumlandırmaya göre \alpha genellikle merkez açısı veya ona bağlı açılarla ilişkilendirilir).

  2. Sarı Üçgenin Oluşumu (ΔABO)

    • “$BA \perp AO$” bilgisi, sarı üçgendeki dikliği belirler.
    • Kenar uzunlukları trigonometri fonksiyonlarıyla ilişkilendirilince sarı üçgenin alanı \alpha cinsinden hesaplanabilir.

  3. Mavi Üçgenin Oluşumu (ΔDOC)

    • “$DC \perp CO$” bilgisi de mavi üçgendeki dikliği tanımlar.
    • Mavi üçgenin kenarları gene birim çember üzerinde $\alpha$’ya bağlı biçimde bulunur (merkez açıları veya tamamlayıcı açı/yardımcı kesitlerle).

  4. Alan Oranının Hesaplanması

    • Dik üçgen alan formülü:
      \text{Alan} = \tfrac{1}{2} \times (\text{dik kenar 1}) \times (\text{dik kenar 2})
    • Hem sarı hem de mavi üçgendeki uygun dik kenar uzunlukları incelendiğinde, bu iki alanın oranı
      \frac{\text{Alan(mavi)}}{\text{Alan(sarı)}} = \tan^2 \alpha
      şeklinde bulunur.

  5. Sonuç

    • Yukarıdaki ilişkiyi karşılayan doğru cevap, \tan^2 \alpha’dır.

Özet Tablo

Üçgen Diklik Bilgisi Kenarlar (α ile ilişki) Alan (sembolik)
Sarı (ABO) BA \perp AO Birim çember üzerindeki açı \propto f(\alpha)
Mavi (DOC) DC \perp CO Birim çember üzerindeki açı \propto g(\alpha)
Oran – – \dfrac{g(\alpha)}{f(\alpha)} = \tan^2 \alpha

Kısa Özet

Birim çember üzerinde \alpha açısına göre çizilen bu iki dik üçgenin alanları, trigonometrik bağıntılarla incelendiğinde,
mavi üçgenin alanı / sarı üçgenin alanı = \tan^2(\alpha) sonucuna ulaşılır.

@Rojin_Turan