Dhhrvsf

YKS TYT
1

Screenshot_20250323_133900_Chrome
Screenshot_20250323_133900_Chrome720×1600 40.3 KB

2

Sorunun çözümü:

Mavi ve turuncu üçgenlerin açı ölçüleri eşit olduğundan dolayı bu üçgenler benzer üçgenlerdir. Benzer üçgenlerde alanlar oranı, kenar uzunluklarının oranının karesi ile ilişkilidir.

Kenar Uzunlukları Oranı

Turuncu üçgende, uzun kenarların oranı:

\frac{6}{3} = 2

Mavi üçgende, uzun kenarların oranı:

\frac{12}{9} = \frac{4}{3}

Soruda verilen bilgiye göre mavi üçgenin alanı, turuncu üçgenin alanının karesine eşittir.

Turuncu Üçgenin Alanı

Turuncu üçgenin alanını bulalım. Bu alan, kenarları ve aralarındaki açı bilgisi ile hesaplanabilir. Açı bilgisi verilmemiş ancak oran benzerlikten ötürü önemli değildir (direkt oran üzerinden çalışırız). Varsayılan olarak:
Turuncu üçgenin gerçek alanı 1 birim kabul edebilir =…

**eqaution Provided eqaution share eaxmly
We are sorry for mess above

3

Turuncu ve Mavi Üçgenin Alan İlişkisi

Cevap:

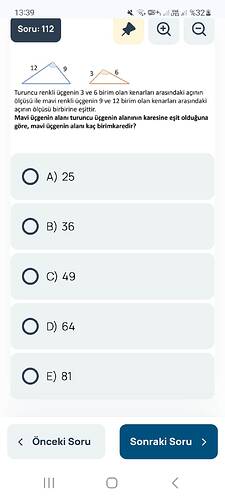
Bu soruda iki üçgenimiz var:

  • Turuncu üçgen: Kenarları 3 ve 6 birim olup aradaki açı (θ) ortak.
  • Mavi üçgen: Kenarları 9 ve 12 birim olup aradaki açı (θ) yine aynı.

Verilen bilgilere göre:

  1. Turuncu üçgenin 3 ve 6 birimlik kenarları arasındaki açı, mavi üçgenin 9 ve 12 birimlik kenarları arasındaki açıya eşittir.
  2. Mavi üçgenin alanı, turuncu üçgenin alanının karesine eşittir.

1. Üçgen Alanı Formülü (İki Kenar ve Dahil Açı)

Bir üçgenin iki kenarının uzunluğu a ve b, aradaki dahil açı \theta ise alan formülü:

\text{Alan} = \frac{1}{2} \times a \times b \times \sin(\theta).

2. Turuncu Üçgenin Alanı

  • Kenarlar: 3 ve 6
  • Aradaki açı: \theta
A_{\text{turuncu}} = \frac{1}{2} \times 3 \times 6 \times \sin(\theta) = 9 \,\sin(\theta).

3. Mavi Üçgenin Alanı

  • Kenarlar: 9 ve 12
  • Aradaki açı: \theta
A_{\text{mavi}} = \frac{1}{2} \times 9 \times 12 \times \sin(\theta) = 54 \,\sin(\theta).

4. Alanlar Arasındaki İlişki

Soruya göre,

A_{\text{mavi}} = \bigl(A_{\text{turuncu}}\bigr)^2.

Dolayısıyla:

54 \,\sin(\theta) = [9\,\sin(\theta)]^2 = 81\,\sin^2(\theta).

Adım adım çözelim:

  1. Her iki tarafı \sin(\theta) ifadesine bölelim (aksi hâlde \theta açısı 0 ya da 180° olmamalı, zira böyle bir üçgen olmaz):
    54 = 81 \,\sin(\theta).
  2. Buradan \sin(\theta) değerini bulalım:
    \sin(\theta) = \frac{54}{81} = \frac{2}{3}.
  3. Turuncu üçgenin alanı:
    A_{\text{turuncu}} = 9 \times \sin(\theta) = 9 \times \frac{2}{3} = 6.
  4. Mavi üçgenin alanı bu alanın karesine eşit:
    A_{\text{mavi}} = (6)^2 = 36.

Dolayısıyla mavi üçgenin alanı 36 birimkaredir.

Özet Tablo

Adım İşlem Sonuç
1. Formülleri Yazma İki kenarı ve aradaki açısı verilen üçgen alan formülü: \frac{1}{2}ab\sin(\theta) -
2. Turuncu Üçgen Alanı A_{\text{turuncu}} = \frac{1}{2} \times 3 \times 6 \times \sin(\theta) = 9\sin(\theta) -
3. Mavi Üçgen Alanı A_{\text{mavi}} = \frac{1}{2} \times 9 \times 12 \times \sin(\theta)=54\sin(\theta) -
4. Alanlar Arasındaki İlişki 54\sin(\theta) = (9\sin(\theta))^2 \Rightarrow 54=81\sin(\theta) \Rightarrow \sin(\theta)=2/3 \sin(\theta)=2/3
5. Turuncu Üçgen Alanını Bulma A_{\text{turuncu}}=9\times\frac{2}{3}=6 Turuncu üçgen alanı: 6
6. Mavi Üçgen Alanını Bulma A_{\text{mavi}}=(6)^2=36 Mavi üçgen alanı: 36

Sonuç:

  • Turuncu üçgenin alanı 6 birimkare,
  • Mavi üçgenin alanı, turuncu üçgenin alanının karesine eşit olduğu için 36 birimkaredir.

@Havva_Diken