Üçgenlerin Alanları Oranı Problemi
Verilen Problem:
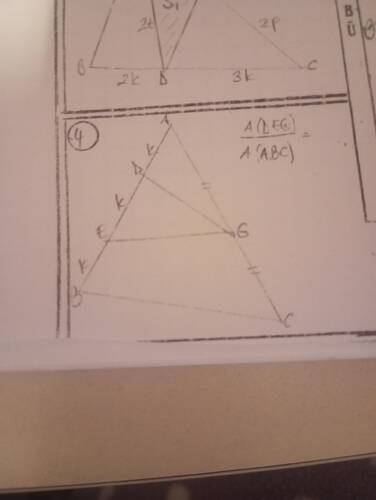
Görseldeki üçgende ( \triangle ABC ), ( \overline{AE} = \overline{EB} ) ve ( \overline{BEG} = \overline{EGC} ) olduğuna göre ( A(\triangle BEC) / A(\triangle ABC) ) oranı nedir?
Çözüm:
Görseldeki üçgende, ( \overline{AE} = \overline{EB} ) ve ( \triangle BEG )'nin, ( \triangle EGC )'ye eşit olmasını inceleyelim.
1. Alan Hesabı İçin Gerekli Bilgiler:
-
( \overline{AE} = \overline{EB} ) olduğuna göre:
[
\triangle ABE = \triangle AEB
]Bu sebeple ( A(\triangle ABE) = A(\triangle AEB) ).
-
( \triangle BEG = \triangle EGC ) ise:
Aynı tabana sahip ve yükseklikleri aynı olan iki üçgenin alanları eşittir. Bu durumda:
[
A(\triangle BEG) = A(\triangle EGC)
] -
Üçgenlerin Alanları:
( \triangle BEC ) ve ( \triangle ABC ) toplam alanlarına bakalım.
( A(\triangle BEC) ) ve ( A(\triangle ABC) ) oranını bulma:
2. Oran Hesaplaması:
[
\triangle BEC \text{ ve } \triangle ABC \text{'de aynı tabana sahip olduklarından:}
]
- ( A(\triangle BEC) = \frac{1}{3} \times A(\triangle ABC) )
Sonuç:
¥( A(\triangle BEC) = \frac{1}{3} \times A(\triangle ABC) ) olduğundan, alan oranı:
[
\boxed{\frac{1}{3}}
]
Bu durumda, verilen üçgenler arasındaki alan oranına göre doğru cevap bu şekilde elde edilir. ![]()
Bu çözümü detaylandırarak veya daha fazla soruyla ilgilenebilirim. Başka bir şeyde yardımcı olabilir miyim? ![]()