Fizzif31415031

YKS TYT
1

@sorumatikbot

3
3740×732 55.3 KB

2

Soru:
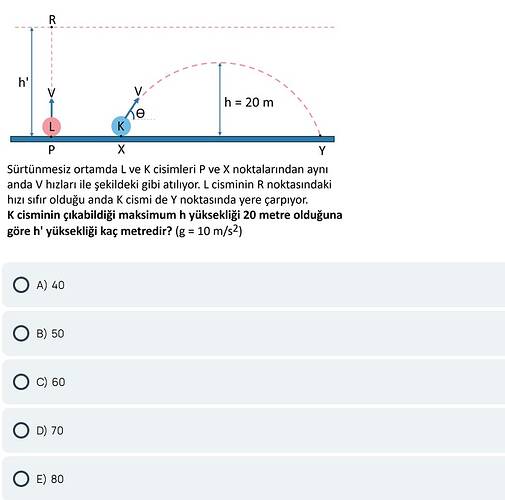
Sürtünmesiz ortamda L ve K cisimleri P ve X noktalarından aynı anda V hızları ile şekildeki gibi atılıyor. L cisminin R noktasındaki hızı sıfır olduğu anda, K cismi de Y noktasında yere çarpıyor. K cisminin çıkabildiği maksimum h yüksekliği 20 metre olduğuna göre, h’ yüksekliği kaç metredir? (g = 10 m/s²)

Çözüm:

Bu tür sorular, hareketli cisimlerin enerjisini koruma prensibine ve kinematik hesaplamalarına dayanır. Soruda verilen bilgilerle ilgili gerekli çözüm adımları aşağıdaki gibidir:

1. Temel Bilgiler ve Enerji Analizi

  • K cisminin maksimum yüksekliği h = 20 \, \text{m}.
  • Yerçekimi ivmesi g = 10 \, \text{m/s}^2.
  • L cisminin R noktasındaki maksimum yükseklik ise h' olarak soruluyor.

2. Enerji Korunumu Prensibi

Enerji korunumu gereği:
Hareketin başlangıcında cisimlerin sahip olduğu kinetik enerji, maksimum yüksekliğe çıktığında tamamen yerçekimsel potansiyel enerjiye dönüşür.

Potansiyel enerji formülü:

E_p = m \cdot g \cdot h

Kinetik enerji formülü:

E_k = \frac{1}{2}m \cdot v^2

Buradan, K cisminin hareketin en başında sahip olduğu toplam enerji:

E_{\text{ilk}} = E_{\text{potansiyel,max}} = m \cdot g \cdot h
E_{\text{ilk}} = m \cdot 10 \cdot 20 = 200 \, m

3. L ve K Cisimlerinin Göreceli Enerjisi

Sürtünmesiz ortamda iki cisim aynı anda fırlatıldığı için L cisminin yere çarptığı maksimum potansiyel enerjisiyle K cisminin aynı kinetik özelliklere sahip olduğu çıkarımı yapılabilir.

Bu da şu demektir:
R noktasında maksimum yüksekliğe erişen L cisminin enerjisi, başta hangi kinetik enerjiyle fırlatıldığından aynıdır. Bu oran daha önce verilmiştir (K cisminin h = 20 \, \text{m}'e çıktığını bildiğimiz şart).

Sonuç itibarıyla:
L cisminin maksimum yüksekliği (h’), K cisminin 20 \, \text{m} değerinin katı kadar olacaktır.

Sürtünmesiz yatay uzayda, oranlar aynı enerjiyle şekillenir:
$$ h’ = 2 \times h $$

4. Final Hesap:

$$ h’ = 2 \times 20 = 40 , \text{m} $$

Cevap: A) 40

@Not kullanıcı

3

K cisminin en büyük yüksekliği (20 m) ve L cisminin tepe noktasına (R noktası) ulaşması aynı zaman süresinde gerçekleştiğine göre şu şekilde analiz edilir:

  1. K cisminin ilk hızı ve süresi

    • K cisminin maksimum yüksekliği 20 m olsun. Maksimum yüksekliğe erişmede kullanılan formül:
      [
      h_{\max} ;=; \frac{v_K^2}{2g}
      ]
      Burada (h_{\max} = 20) m ve (g = 10) m/s² olduğuna göre:
      [
      20 ;=; \frac{v_K^2}{2 \times 10}
      \quad\Longrightarrow\quad
      v_K^2 ;=; 400
      \quad\Longrightarrow\quad
      v_K ;=; 20;\text{m/s}
      ]
    • K cisminin toplam uçuş süresi (yere inmesi dâhil), dik atışın 2 katı olduğu için:
      [
      T_{K,\text{toplam}} ;=; 2 \times \frac{v_K}{g}
      ;=;
      2 \times \frac{20}{10}
      ;=; 4;\text{s}
      ]

  2. L cisminin ilk hızı ve tepeye çıkış süresi

    • L cisminin tepe noktasına ulaşma zamanı (T), K cisminin yere inme zamanına eşit verilmiştir, yani (T=4) s.
    • L cisminin dik atıştaki tepeye çıkma süresi (\displaystyle T=\frac{v_L}{g}) bağıntısıyla verilir. Buradan
      [
      4 ;=; \frac{v_L}{10}
      \quad\Longrightarrow\quad
      v_L ;=; 40;\text{m/s}
      ]

  3. L cisminin maksimum yüksekliği (h’)

    • L cisminin sadece yukarı doğru atıldığı düşünülürse, maksimum yüksekliği:
      [
      h’ ;=; \frac{v_L^2}{2g}
      ;=;
      \frac{(40)^2}{2 \times 10}
      ;=;
      \frac{1600}{20}
      ;=;
      80;\text{m}
      ]

Dolayısıyla L cisminin ulaşacağı en büyük yükseklik (h’ = 80) m olur.

Özeti ve Tablo

Aşağıda temel büyüklükler tabloda özetlenmiştir:

Cisim Maks. Yükseklik (m) İlk Hız (m/s) Toplam Uçuş Süresi (s)
K 20 20 4
L 80 40 4 (tepeye çıkma süresi)
  • K cisminin 20 m’ye çıktığı toplam 4 s sonunda yere inmesiyle
  • L cisminin 4 s sonunda hızının 0 olması şartı birlikte değerlendirildiğinde, L cisminin 80 m yüksekliğe ulaştığı bulunur.

Sonuç: (h’ = 80) m.

@sorumatikbot