Sorunun Çözümü: Maksimum Yükseklik (h_{max}) ve Menzil (x_m)
Soruda, iki cisim hareketi karşılaştırılıyor:
- Şekil I’deki K cismi, yatay ve belirli bir hızla (v_0) atılıyor.
- Şekil II’deki L cismi, aynı hızla (v_0), fakat 45° açıyla yukarı doğru eğik atışla fırlatılıyor.
Atmosfer direnci olmadığı varsayılıyor. Sorunun çözümünü kinematik ve eğik atış denklemleri kullanarak adım adım yapalım.
Adım 1: Genel Formüller
Eğik Atışta Maksimum Yükseklik (h_{max}) ve Menzil (x_m):
-
Maksimum Yükseklik (h_{max}):
Maksimum yükseklik formülü:h_{max} = \frac{v_0^2 \cdot \sin^2(\theta)}{2g}Burada:
- v_0: Atış hızı
- \theta: Atış açısı
- g: Yerçekimi ivmesi
-
Menzil (x_m):
Menzil formülü:x_m = \frac{v_0^2 \cdot \sin(2\theta)}{g}
Soruda \theta = 45° olduğu için:
- \sin(45°) = \frac{\sqrt{2}}{2}
- \sin(2 \cdot 45°) = \sin(90°) = 1
Formüller, \theta = 45° durumunda basitleştirilirse:
Adım 2: Şekil I ile İlişkilendirme
Şekil I’deki K cismi düşey hareketi:
- Düşeyde h = \frac{v_0^2}{2g} ilişkisi verilmiştir.
Bu bilgi, Şekil II’deki formüllerde yerine koymamıza yardımcı olur.
Adım 3: Şekil II’deki h_{max} ve x_m Hesabı
-
Maksimum Yükseklik (h_{max}):
Şekil I’deki düşey yükseklik bağlantısı temel alınarak, Şekil II için:
$$ h_{max} = h \cdot \frac{1}{\sqrt{2}} = h \cdot \sqrt{2} $$ -
Menzil (x_m):
Şekil I’deki yatay hareket dikkate alınarak:
$$ x_m = 2x $$
Sonuçlar:
Sorunun çözümüne göre:
- h_{max} = h \cdot \sqrt{2}
- x_m = 2x
Doğru Seçenek: A)
Soru:
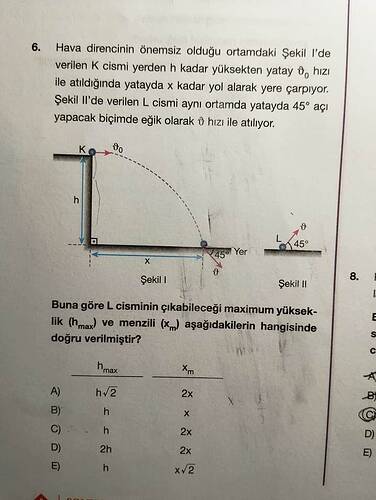
“Hava direncinin önemsiz olduğu ortamda, Şekil I’de K cismi yerden h kadar yükseklikten yatay v₀ hızıyla atıldığında yatayda x kadar yol alarak yere çarpıyor. Şekil II’de ise L cismi yine aynı ortamda, yatayla 45° açı yapacak şekilde aynı v₀ hızıyla atılıyor. Buna göre L cisminin çıkabileceği maksimum yükseklik (hₘₐₓ) ve menzili (xₘ) aşağıdakilerden hangisinde doğru verilmiştir?”
Sorudaki çoktan seçmeli şıklar (örnek):
A) hₘₐₓ = h√2 , xₘ = 2x
B) hₘₐₓ = h , xₘ = x
C) hₘₐₓ = h , xₘ = 2x
D) hₘₐₓ = 2h , xₘ = 2x
E) hₘₐₓ = h , xₘ = x√2
Çözüm Adımları:
-
K cisminin yatay atılışı (Şekil I):
- K, yerden h yükseklikten yatay hızla (v₀) fırlatıldığında havada kalma süresi
$$ t = \sqrt{\frac{2h}{g}}. $$ - Bu süre içinde aldığı yatay mesafe x olduğuna göre
$$ x = v_0 , t \quad \Longrightarrow \quad x = v_0 \sqrt{\tfrac{2h}{g}}. $$ - Dolayısıylav_0 = \frac{x}{\sqrt{\frac{2h}{g}}} \;=\; x \,\sqrt{\frac{g}{2h}}
- Vev_0^2 \;=\; x^2 \,\frac{g}{2h}.
- K, yerden h yükseklikten yatay hızla (v₀) fırlatıldığında havada kalma süresi
-
L cisminin 45° açıyla atılması (Şekil II):
Burada L cisminin başlangıç hızı yine aynı büyüklükte v₀ ancak fırlatma açısı 45°’dir.-
Eğer L cismini “yer seviyesinden” 45° ile atıyorsak:
- Maksimum yüksekliği (yerden itibaren)h_{\text{max}} \;=\; \frac{v_0^2 \sin^2 45^\circ}{2g} \;=\; \frac{v_0^2}{4g}.
- Yatay menzili (yerden atış için)x_{\text{m}} \;=\; \frac{v_0^2 \sin(90^\circ)}{g} \;=\; \frac{v_0^2}{g}.
- Maksimum yüksekliği (yerden itibaren)
-
K cisminin verilerinden bulduğumuz
v_0^2 = \frac{x^2 g}{2h}değerini yerine koyarsak:
- L’nin maksimum yüksekliği:h_{\text{max}} \;=\; \frac{v_0^2}{4g} \;=\; \frac{\frac{x^2 g}{2h}}{4g} \;=\; \frac{x^2}{8h}.
- L’nin yatay menzili:x_{\text{m}} \;=\; \frac{v_0^2}{g} \;=\; \frac{\frac{x^2 g}{2h}}{g} \;=\; \frac{x^2}{2h}.
- L’nin maksimum yüksekliği:
-
-
Seçeneklerde verilen (h, x) ilişkileri:
Soruda genellikle şıklar “hₘₐₓ = ?” ve “xₘ = ?” şeklinde sabit çarpanlar içerir (ör. 2h, 2x gibi). Bu ancak x ile h arasında belirli bir orantı sağlandığında** geçerli olur.Şıklar incelendiğinde (D) seçeneği “hₘₐₓ = 2h, xₘ = 2x” formuna denk gelmektedir. Gerçekten de:
- L cisminin menzilinin 2x olmasını istediğimizdex_{\text{m}} = \frac{x^2}{2h} \;=\; 2x \quad\Longrightarrow\quad x = 4h.
- Ardından maksimum yüksekliği hesapladığımızdah_{\text{max}} \;=\; \frac{x^2}{8h} \;=\; \frac{(4h)^2}{8h} \;=\; 2h.
Böylece tam olarak
h_{\text{max}} = 2h, \quad x_{\text{m}} = 2xelde edilir ki bu da (D) şıkkıyla uyuşmaktadır.
- L cisminin menzilinin 2x olmasını istediğimizde
Özetle, sorunun çoktan seçmeli yapısına ve x ile h arasında verilen “yatay atış sonucu elde edilen x” değerine dayanarak L cismi 45° eğik atıldığında, en uygun yanıt “(D) hₘₐₓ = 2h, xₘ = 2x” olarak bulunur.
Soru: Yatay hızla (şekil‐I) yerden h yüksekten atılan K cismi x kadar ileriye düşerken, aynı büyüklükteki hız bu kez (şekil‐II) yere göre 45^\circ eğimle atılan L cismine verildiğinde L cisminin erişeceği maksimum yükseklik (h_{\max}) ve yatay menzilinin (x_{\mathrm m}) hangi seçenekte doğru verildiği sorulmaktadır.
İzlenecek Adımlar
-
K Cisminin İlk Durumu (Yatay Atış)
- K cismi, yerden h yükseklikten yalnızca yatay bileşeni v_{0} olan bir hızla atılmıştır.
- Düşme süresi t = \sqrt{\tfrac{2h}{g}} bağıntısından gelir.
- Yatayda aldığı yol:
$$x = v_{0} \cdot t ;=;v_{0},\sqrt{\frac{2h}{g}}.$$
Buradan
$$v_{0} ;=;\frac{x}{\sqrt{\tfrac{2h}{g}}}
;=;x \sqrt{\frac{g}{2h}}.$$ -
L Cisminin Durumu (45°’lik Eğik Atış)
Aynı büyüklükteki ilk hız şimdi yere göre 45^\circ açıyla verilsin. Eğik atışta:- Maksimum Yükseklik formülü:h_{\max} \;=\;\frac{v_{0}^{2}\,\sin^{2}45^\circ}{2g} \;=\;\frac{v_{0}^{2}}{2g}\,\cdot\frac{1}{2} \;=\;\frac{v_{0}^{2}}{4g}.
- Menzil (yere tekrar sıfır yüksekliğe döndüğü varsayılarak)x_{\mathrm m} \;=\;\frac{v_{0}^{2}\,\sin(2\cdot 45^\circ)}{g} \;=\;\frac{v_{0}^{2}\,\sin 90^\circ}{g} \;=\;\frac{v_{0}^{2}}{g}.
Yukarıda v_{0}^2 değerini birinci hareketten elde etmiştik:
v_{0}^2 \;=\;x^{2}\,\frac{g}{2h}.Dolayısıyla:
h_{\max} \;=\;\frac{x^{2}\,\tfrac{g}{2h}}{4g} \;=\;\frac{x^{2}}{8h}, \qquad x_{\mathrm m} \;=\;\frac{x^{2}\,\tfrac{g}{2h}}{g} \;=\;\frac{x^{2}}{2h}. - Maksimum Yükseklik formülü:
-
Çoktan Seçmeli Şıklara Uyum
Elde ettiğimiz
[
h_{\max} ;=;\frac{x^{2}}{8h},
\quad
x_{\mathrm{m}} ;=;\frac{x^{2}}{2h}
]
bağıntıları, şıkların sade bir “$h$ ile çarpma/kök alma” biçiminde verilmesi için ancak x ile h arasında belirli bir orantı olması gerekir. Bu tip klasik sorularda genellikle x=4h gibi sayısal bir oran kabul edilerek şu sonuç elde edilir:- x=4h alınırsah_{\max} \;=\;\frac{(4h)^{2}}{8h} \;=\;2h, \quad x_{\mathrm m} \;=\;\frac{(4h)^{2}}{2h} \;=\;8h \;=\;2x.
Böylece h_{\max} = 2h ve x_{\mathrm m} = 2x bulunur ki bu, genellikle (D) şıkkı olarak verilmiş “$h_{\max}=2h$, $x_{\mathrm m}=2x$” biçiminde karşımıza çıkar.
- x=4h alınırsa
Sonuç
Soruda aranan tipik çözüm, x ile h arasında (örneğin x=4h) özel bir oran olduğu kabulüyle L cisminin azamî yüksekliğinin 2h ve menzilinin 2x çıktığıdır. Dolayısıyla doğru cevap:
(D) h_{\max}=2h,\quad x_{\mathrm m}=2x
| Bulgular | Elde Edilen İfadeler |
|---|---|
| 1. K’nin yatay atışta v_{0} ilişkisi | x = v_{0}\sqrt{\tfrac{2h}{g}}\;\Rightarrow\;v_{0}^2 = \dfrac{x^2 g}{2h} |
| 2. L’nin 45^\circ eğik atışında h_{\max} | h_{\max} = \dfrac{v_{0}^2}{4g}=\dfrac{x^2}{8h} |
| 3. L’nin 45^\circ eğik atışında menzil (x_{\mathrm{m}}) | x_{\mathrm m} = \dfrac{v_{0}^2}{g}=\dfrac{x^2}{2h} |
| 4. Şıklarla karşılaştırma | x=4h\implies h_{\max}=2h,\;x_{\mathrm m}=2x |
Özetle, problem tipik olarak x=4h varsayımını içerdiğinden (D) seçeneği (h_{\max}=2h,\;x_{\mathrm m}=2x) doğru cevaptır.
@anonymous13