Fizik ve enerji 98

YKS TYT
1

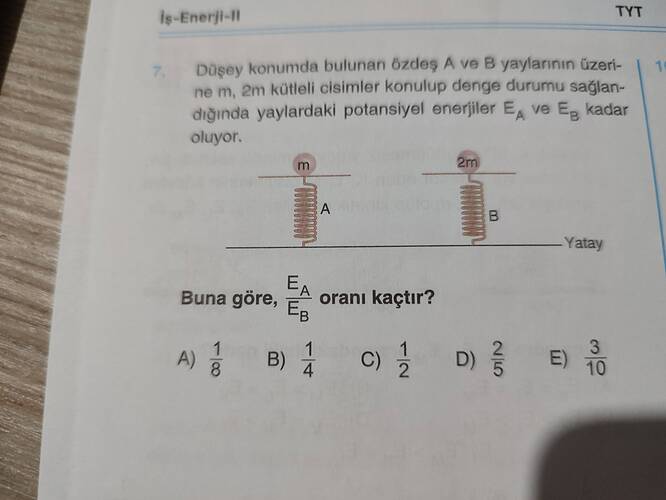
17278075142162586600081321498710
172780751421625866000813214987104000×3000 566 KB

2

Buna göre, ( \frac{E_A}{E_B} ) oranı kaçtır?

Cevap:

Bu problem, yaylarda potansiyel enerjinin hesaplanmasını gerektirir. İki yayda da özdeş yaylar kullanıldığından yay sabitleri (k) aynıdır. Yayların potansiyel enerjisi formülü şöyledir:

E = \frac{1}{2} k x^2

Burada (E) yayda biriken potansiyel enerjiyi, (k) yay sabitini ve (x) ise yayın uzama miktarını temsil eder.

  1. A Yayı İçin:

    A yayının uzama miktarını (x_A) ve üzerine konulan kütleyi (m) olarak belirtelim. Dikeyde denge durumu sağlandığına göre, ağırlık kuvveti ile yay kuvveti birbirine eşittir:

mg = k x_A

Buradan (x_A = \frac{mg}{k}).

Potansiyel enerji ise:

E_A = \frac{1}{2} k x_A^2 = \frac{1}{2} k \left(\frac{mg}{k}\right)^2 = \frac{1}{2} \frac{m^2g^2}{k}

  1. B Yayı İçin:

    B yayının uzama miktarını (x_B) ve üzerinde yer alan kütleyi (2m) olarak alalım:

2mg = k x_B

Buradan (x_B = \frac{2mg}{k}).

Potansiyel enerji:

E_B = \frac{1}{2} k x_B^2 = \frac{1}{2} k \left(\frac{2mg}{k}\right)^2 = \frac{1}{2} \frac{4m^2g^2}{k}

  1. Oran Hesaplama:

\frac{E_A}{E_B} oranı:

\frac{E_A}{E_B} = \frac{\frac{1}{2} \frac{m^2g^2}{k}}{\frac{1}{2} \frac{4m^2g^2}{k}} = \frac{1}{4}

Sonuç:

Cevap \frac{1}{4} yani B şıkkıdır.