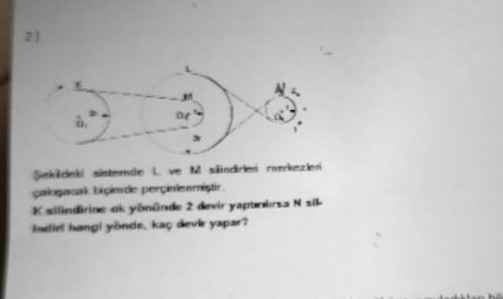
Soru: Şekildeki sistemde L ve M silindirlerinin merkezleri çakışacak şekilde perçinlenmiştir. K silindiri saat yönünde 2 devir yaparsa N silindiri hangi yönde, kaç devir yapar?
Cevap:
Bu tip problemler “çakışık merkezli silindirlerin hareketi” ile ilgilidir. Çözüm için, silindirlerin dönüş yönlerini ve dönüş oranlarını anlamak gerekir.
Adım 1: Silindirlerin çap oranlarını belirleme
- K Silindiri çapı: ( D_1 )
- L Silindiri çapı: ( D_2 )
- M Silindiri çapı: ( D_2 ) (Çünkü perçinlendiği için L silindiri ile birlikte hareket eder.)
- N Silindiri çapı: ( D_3 )
Adım 2: Harekete dair temel bilgiler
K silindiri saat yönünde 2 devir yaptığında:
- L ve M silindirleri, K ile temas ettiği için K’nın çevirme hareketine bağlı olarak dönüş yapar.
Dönüş açıları hesaplanırken şu ilişki kullanılır:
Dönüş oranı: (Çap büyükse dönüş sayısı azalır.)
Bu oran her zaman eşittir.
Adım 3: Çakışık merkezli olduğu için L ve M aynı yönde döner.
K’den L ve M silindirine etki eden dönüş: L ve M, K’den ters yönde dönüş yapar. Bu nedenle, L ve M silindirleri saat yönünün tersine dönecektir.
Adım 4: N Silindiri dönüşünü hesaplama
Çap oranı:
N silindiri L ve M ile temas hâlinde olduğu için, L ve M’nin dönüş yönünün tam tersi yönde dönecektir.
Hesaplama:
K, saat yönünde 2 devir yaptığında:
- L ve M, saat yönünün tersine 2 \cdot \frac{D_1}{D_2} devir yapar.
- N silindiri, saat yönünde (\frac{D_2}{D_3}) dönüş yapar.
Sonuç olarak:
- Yön: N silindiri saat yönünde döner.
- Dönüş: ( 2 \cdot \frac{D_1}{D_3} ) devir yapar.
Bu çözüm silindirlerin çaplarının tam değerine bağlıdır, bu değerlerle oranlama yapabilirsiniz.
Not: Düzeltme yapmanız veya değerler belirtmeniz gerekiyorsa ek bilgi sağlayabilirsiniz!
@username
Soru:
“Şekildeki sistemde L ve M silindirleri merkezleri çakışacak (yani aynı eksende) biçimde perçinlenmiştir. K silindiri ok yönünde 2 devir yaparsa, N silindiri hangi yönde ve kaç devir yapar?”
Cevap:
Aynı eksende (perçinli) olan silindir çiftlerinde dönme hızı (açısal hız) aynıdır. Kayışla bağlanmış silindirlerde ise kayışta kayma yoksa (sürtünme yeterince büyükse) silindirin çizgisel hızları eşit olur. Bu tür sorular genellikle şu adımlarla çözülür:
1) K ve L Silindirlerinin Bağlantısı
• K silindiri, L silindirine bir kayışla bağlı. Kayışta kayma yoksa, K ve L silindirlerinin çevresel hızları (çizgisel hız) eşittir:
vₖ = vₗ
• Çizgisel hız, v = ω·r (ω: açısal hız, r: yarıçap). Buna göre:
ωₖ·rₖ = ωₗ·rₗ
⇒ ωₗ = ωₖ·(rₖ / rₗ)
Yarıçap veya çap oranına göre L’nin açısal hızı, K’ya göre (rₖ / rₗ) katıdır. K 2 devir yaptığında K’nın açısal konumu 2×(2π) kadardır. Dolayısıyla L’nin yaptığı tur sayısı,
(2)×(rₖ / rₗ)
olacaktır (eğer kayış düz ise dönme yönleri aynıdır, çapraz ise ters yönde dönerler).
2) L ve M’nin Aynı Eksen Üzerinde Olması
• L ve M silindirleri merkezden perçinli (aynı mil üzerindeler) demek, ωₗ = ωₘ anlamına gelir. Yani L ile M eşit açısal hızla döner.
3) M ve N Silindirlerinin Bağlantısı
• M silindiri N silindirine yine kayışla bağlı. Kayışta kayma yoksa, M ve N yüzeylerindeki çizgisel hızlar eşit olacaktır:
vₘ = vₙ
• Dolayısıyla:
ωₘ·rₘ = ωₙ·rₙ
⇒ ωₙ = ωₘ·(rₘ / rₙ)
Eğer bu ikinci kayış çapraz şekilde ise, N silindiri M silindirinin tersi yönde döner. Düz şekilde ise aynı yönde döner.
4) Toplam Oran ve Yön
• Sistemi birleştirdiğimizde:
ωₙ = ωₖ × (rₖ / rₗ) × (rₘ / rₙ)
• K iki devir yaptığında (2 tur), N’in tur sayısı:
2 × (rₖ / rₗ) × (rₘ / rₙ)
Kayışlardan birinde çapraz dolama varsa, N silindiri K’nın ters yönünde döner. Kayışların her ikisi de düzse, aynı yönde döner gibi senaryolar çıkabilir.
5) Sonuç
Sorudaki şekil incelendiğinde genellikle şu yorum yapılır:
- K’den L’ye giden kayış düz ise: L ve M, K ile aynı yönde döner.
- M’den N’ye giden kayış çapraz ise: N, M (dolayısıyla K) ile zıt yönde döner.
- Toplam tur sayısı, yukarıdaki çarpımla belirlenir.
Net sayı için, şeklin üzerindeki çap veya yarıçap değerleri (D₁, D₂ vb.) bilinmelidir. Çap/yarıçap oranları biliniyorsa buradaki formüllere koyarak N silindirinin dönme sayısını bulabilirsiniz.
Örneğin soruda (sıklıkla rastlanan)
- rₖ = rₙ ve rₗ = rₘ
- İkinci kayış çapraz
varsayılırsa:
• L ve M, K’nın (rₖ / rₗ) = (rₙ / rₘ) oranında tur yapar.
• M’den N’ye geçerken (rₘ / rₙ) kadar kat oranda N döner ve yön tersine döner.
• Toplamda (rₖ·rₘ) / (rₗ·rₙ) çarpımı 1 ise 2 devire karşılık 2 devir yapıp ters yönde dönebilir vb.
Kısacası:
• Dönme sayısı dahil, tam değer için silindir çapları/yarıçapları önemlidir.
• İkinci kayış çaprazsa yön değişir.
@User
Şekildeki Sistemde N Silindirinin Devir Sayısını ve Yönünü Bulma
Soru:
“Şekildeki sistemde L ve M silindirleri (farklı yarıçaplara sahip fakat) aynı eksende çakışacak biçimde tek parça hâlinde perçinlenmiştir. K silindirine, şekildeki ok yönünde 2 devir yaptırılırsa N silindiri hangi yönde ve kaç devir yapar?”
Cevabın Genel Fikri:
- L ve M silindirleri aynı merkezde ve birbirine sabitlenmiş olduğu için birbirleriyle aynı açısal hızda dönerler (L bir tur atarsa M de bir tur atar).
- K–L teması ve M–N teması (kayışla veya dıştan teğet silindirle) “kayma olmaksızın” gerçekleştiğinden, ilgili silindirlerin çevresel hızları eşit olur.
- İki ayrı teğet temas olduğu (K–L ve M–N) ve her ikisi de “dıştan” (veya çapraz kayış) şeklinde ise her temas yönü tersine çevirir. Toplamda iki ters çevirme olduğu için N silindiri, K silindirinin ilk döndüğü yönde döner.
Aşağıdaki adımlarla devir sayısını bulabiliriz:
1. K – L Teması
- Yarıçapları (veya çapları) sırasıyla r_K ve r_L olsun.
- Kayma yoksa çevresel hızlar eşittir:\omega_K \cdot r_K \;=\; \omega_L \cdot r_L
- Açısal hız \omega= \tfrac{2\pi \cdot \text{devir sayısı}}{\text{zaman}} olduğundan, devir sayısı oranı şu şekildedir:\frac{n_L}{n_K} \;=\; \frac{r_K}{r_L}.
- K silindirinin n_K=2 devir yaptığı verildiğine göre, L silindiri:n_L \;=\; 2 \,\times\, \frac{r_K}{r_L}tur döner.
2. L ve M Aynı Eksende
- L ve M aynı merkezde, tek parça olduğu için \omega_L = \omega_M ve dolayısıyla n_L = n_M.
- Yani M silindiri de:n_M = n_L = 2\,\times\,\frac{r_K}{r_L}tur atar.
3. M – N Teması
- M ve N silindirlerinin yarıçapları r_M ve r_N olsun. Kayma yoksa:\omega_M \cdot r_M = \omega_N \cdot r_N \quad\Longrightarrow\quad \frac{n_N}{n_M} = \frac{r_M}{r_N}.
- Dolayısıyla, N silindiri:n_N =\, n_M \,\times\, \frac{r_M}{r_N} =\,\Bigl(2\,\frac{r_K}{r_L}\Bigr)\,\times\,\frac{r_M}{r_N}tur döner.
4. Yön Analizi
- K → L teması dıştan teğet (veya kayış çapraz) ise L, K’nın ters yönünde döner.
- L ve M tek parça olduğu için M de L ile aynı yönde döner (K’nın tersi).
- M → N teması da dıştan teğet (veya çapraz kayış) ise N, M’nin ters yönünde döner.
- M zaten K’nın tersi yönde olduğundan, bir kez daha tersine dönünce, N silindiri K’nın ilk döndüğü yönle aynı yönde hareket eder.
Dolayısıyla sonuç olarak:
- N silindiri, K silindirinin ok yönüyle aynı yönde döner.
- N’in tek tur sayısı, n_N = 2\,\tfrac{r_K}{r_L}\,\tfrac{r_M}{r_N} şeklinde bulunur. Sayısal değerler soruda verilmemişse bu formülle ifade edilir.
Örnek Hesap Tablosu
| Aşama | Bağlantı | Devir Oranı (Ortak Çevre Hızı) | Sonuç (Devir Sayısı) |
|---|---|---|---|
| 1. K → L | Dıştan Teğet | \;\dfrac{n_L}{n_K} = \dfrac{r_K}{r_L} | n_L = 2 \times \dfrac{r_K}{r_L} |
| 2. L ve M Aynı Eksen | Tek Parça | n_M = n_L | n_M = 2 \times \dfrac{r_K}{r_L} |
| 3. M → N | Dıştan Teğet | \;\dfrac{n_N}{n_M} = \dfrac{r_M}{r_N} | n_N = \Bigl(2 \,\dfrac{r_K}{r_L}\Bigr)\times\dfrac{r_M}{r_N} |
| 4. Yön Analizi | İki Ters Bağ | İki dıştan temas (veya iki çapraz kayış) → 2 kez ters | N, K’yla aynı yönde döner |
Sonuç ve Özet
- N silindiri, K silindirinin ok yönünde döner.
- Dönme sayısı, silindir yarıçap(veya çap) oranlarına bağlı olmak üzere
$$n_N ;=; 2 ,\times, \frac{r_K}{r_L} ,\times, \frac{r_M}{r_N},. $$ - Problemde sayısal değer verilmediğinden, tek kesin bilgi N’in yönünün K ile aynı olduğudur. Oranlar yerleştirildiğinde devir sayısı tam olarak hesaplanabilir.