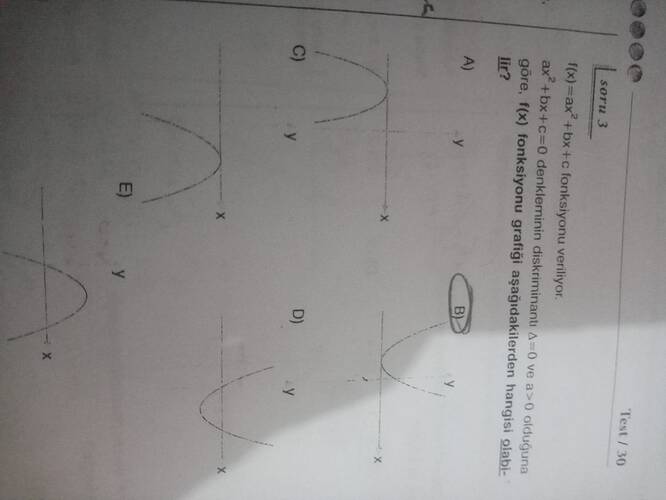
Görüntüde, ikinci dereceden bir fonksiyonun grafiğini inceleyen bir soru var.
Fonksiyon Grafikleri
1. İkinci Dereceden Fonksiyon (Parabol)
Bir ikinci dereceden fonksiyonun genel denklemi şu şekildedir:
f(x) = ax^2 + bx + c
Burada, a, b, ve c sabit sayılardır ve a \neq 0 olmak zorundadır. Bu fonksiyonun grafiği bir parabol şeklinde olur.
2. Diskriminant ve Kökler
Denklemin diskriminantı (D), köklerin doğasını belirler ve şu şekilde hesaplanır:
\Delta = b^2 - 4ac
- \Delta > 0: İki farklı gerçek kök. Parabol x-eksenini iki farklı noktada keser.
- \Delta = 0: Çift katlı bir kök. Parabol x-eksenine teğet olur.
- \Delta < 0: Gerçek kök yok. Parabol x-eksenini kesmez.
3. Verilen Bilgilere Göre Sonuç
Soruda, \Delta = 0 ve a > 0 olduğu belirtiliyor. Bu durumda:
- Parabol tepe noktası, x-eksenine teğet olur.
- Grafiği yukarı doğru açık olur.
Görselde bu duruma uyan grafik seçeneği belirlenmiş.
4. Seçenek Belirleme
- Yukarı Açık Parabol: a > 0
- X-Eksenine Teğet: \Delta = 0
Bu koşullara uygun grafik, yukarı yönlü ve x-eksenine sadece bir noktada teğet olan grafiktir. B seçeneği doğru grafiği göstermektedir.