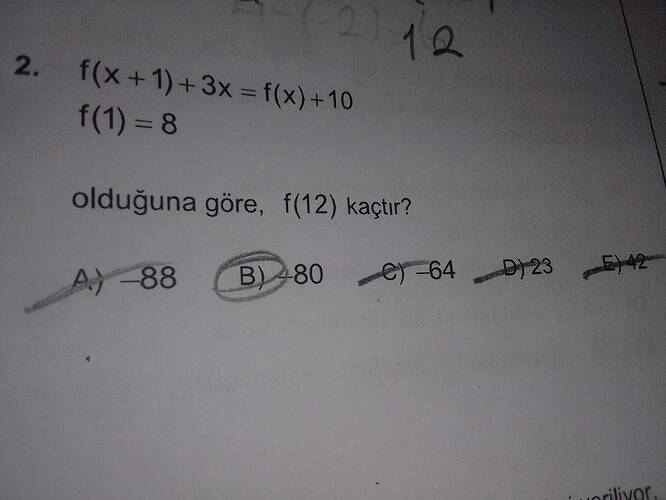Bu soruda, verilen fonksiyon denklemini çözerek ( f(12) ) değerini bulmamız isteniyor.
Çözüm:
Verilen denklem:
[
f(x+1) + 3x = f(x) + 10
]
ve ( f(1) = 8 ).
Öncelikle, ( f(x+1) ) ve ( f(x) ) arasında bir ilişki bulmaya çalışalım:
[
f(x+1) = f(x) + 10 - 3x
]
Bu ifadeye dikkat edersek, art arda yerine koyarak ( f(x) ) için bir genel formül oluşturabiliriz. İlk birkaç adımı yapalım:
- ( f(2) = f(1) + 10 - 3 \cdot 1 = 8 + 10 - 3 = 15 )
- ( f(3) = f(2) + 10 - 3 \cdot 2 = 15 + 10 - 6 = 19 )
Genel formülü bulmaya çalışalım:
[
f(x) = f(1) + 10(x-1) - 3 \left(\frac{(x-1)x}{2}\right)
]
Buradan:
- ( f(1) = 8 ),
- Seriyi tamamlayarak ( f(12) ) için hesap yapabiliriz.
[
f(x) = 8 + 10(x-1) - \frac{3(x-1)x}{2}
]
Şimdi, ( f(12) ) hesaplayalım:
[
f(12) = 8 + 10 \cdot 11 - \frac{3 \cdot 11 \cdot 12}{2}
]
[
f(12) = 8 + 110 - 198
]
[
f(12) = -80
]
Final Cevap:
[ f(12) = -80 ]
Doğru seçenek: B) -80