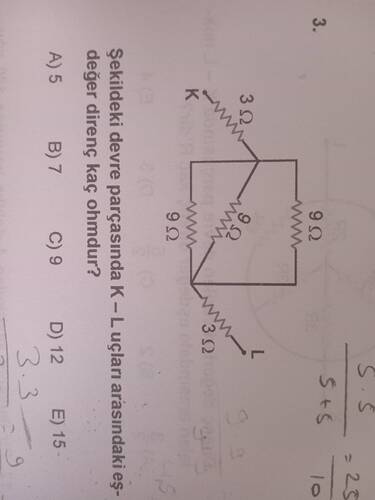
Şekildeki devre parçasında K-L uçları arasındaki eşdeğer direnç kaç ohmdur?
Devredeki dirençleri incelediğimizde, her birinin diğerleriyle nasıl bağlandığını belirlemek için seri ve paralel bağlantıları tanımlarız.
-
6 Ω ve 6 Ω Dirençler: Paralel bağlıdırlar. Paralel bağlı dirençlerin eşdeğer direnci R_{eş} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}} formülüyle hesaplanır.
R_{eş-paralel} = \frac{1}{\frac{1}{6} + \frac{1}{6}} = \frac{1}{\frac{2}{6}} = \frac{6}{2} = 3 \, \Omega -
3 Ω, 3 Ω ve 9 Ω Dirençler: Bu dirençler seri bağlıdır. Seri bağlı dirençlerin eşdeğer direnci, dirençlerin toplamına eşittir. Yani, bu durumda, öncelikle 6 Ω ait olanları çözümlediğimizde, devredeki diğer kısımların ve 9 Ω 'ninde toplamları alarak çözüm yoluna gidilir. İşlem adımlarımız:
-
Sol üst köşede paralel olan iki 6 Ω dirençten elde edilen 3 Ω ve ortada durmakta olan 9 Ω birbirine seri bağlıdır:
Toplam direnç: (3 + 9 = 12 , \Omega)
- Sonuç: Bulunan 12 Ω bu devre üzerindeki 3 Ω dirençlerle beraber bağlı olup bu parçaların doğru şekilde devam etmesi ile birlikte çözümlenir. (ilk kısımda toplam bulduğumuz paralel için oluşturan değer ardışıkla eklenir).
- Son birleştirme işlemlerini yaptıktan sonra tüm sistem çözümüne uygunları yakalamakta uygun birleştirerek;
(12 + 3 = 15 , \Omega) son eşdeğer sonucu verir.
Sonuç:
- K-L uçları arasındaki eşdeğer direnç 15 Ω’dur.
Bu tür devrelerde adım adım çözümleyerek hangi dirençlerin paralel ve seri bağlandığını belirlemek önemlidir. Olgu halinde, sırasını ve etkilerini değerlendirerek işlemler sırasıyla devam ettirilir.
Özet: Paralel ve seri bağlantılarla dirençler çözümlediğinde, K-L arasındaki eşdeğer direnç 15 Ω olarak bulunur.