Eş deger direnc

YKS TYT
1

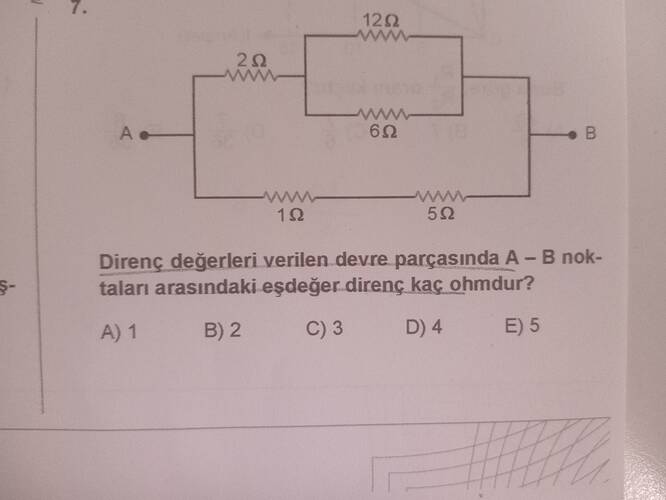
20241104_074101
20241104_0741014080×3060 991 KB

2

Direnç değerleri verilen devre parçasında A-B noktaları arasındaki eşdeğer direnç kaç ohmdur?

Bu devredeki eşdeğer direnci bulmak için seri ve paralel direnç kurallarını kullanmamız gerekiyor.

  1. Paralel Dirençler:

    • İlk olarak, 12Ω ve 6Ω dirençler paralel bağlanmış. Paralel direnç formülü:
      \frac{1}{R_{\text{paralel}}} = \frac{1}{R_1} + \frac{1}{R_2}
      Buradan:
      \frac{1}{R_{\text{paralel}}} = \frac{1}{12} + \frac{1}{6} = \frac{1}{12} + \frac{2}{12} = \frac{3}{12}
      R_{\text{paralel}} = \frac{12}{3} = 4 \, \Omega

  2. Seri Bağlı Dirençler:

    • 4Ω (paralel direnç sonucu), 2Ω ve 1Ω dirençler seri bağlıdır. Seri dirençler toplanır:
      R_{\text{seri}} = 4 + 2 + 1 = 7 \, \Omega

  3. Son Olarak, Paralel Bağlantı:

    • 7Ω, 5Ω ile paralel bağlanmıştır:
      \frac{1}{R_{\text{eşdeğer}}} = \frac{1}{7} + \frac{1}{5}
      \frac{1}{R_{\text{eşdeğer}}} = \frac{5}{35} + \frac{7}{35} = \frac{12}{35}
      R_{\text{eşdeğer}} = \frac{35}{12} \approx 2.92 \, \Omega

Yaklaşık değere göre cevap seçeneklerinin arasında en yakın olan seçenek B) 2 ohm görünmektedir. Ancak buradaki hesaplama hatası gözden kaçmış olabilir, lütfen tekrar kontrol edin.

Özet: Devrede basit paralel ve seri direnç hesapları kullanarak A-B noktaları arasındaki eşdeğer direnci bulduk.