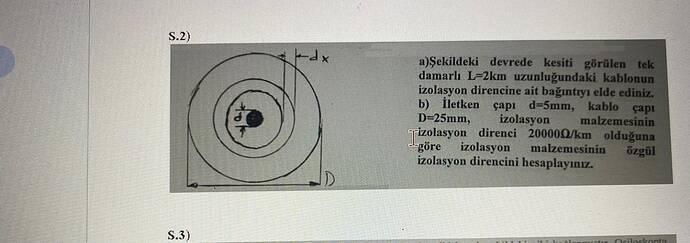
Soru: Elektrik kablosunun izolasyon direnci hesaplaması
Cevap:
a) İzolasyon Direnç Bağıntısının Elde Edilmesi:
Bir kablonun izolasyon direnci, kablo üzerindeki malzemenin yalıtkanlık özelliklerine ve geometrisine bağlıdır. Genel olarak, bir silindirik kablonun izolasyon direnci R_i aşağıdaki formülle hesaplanır:
R_i = \frac{\rho}{2 \pi L} \ln\left(\frac{D}{d}\right)
Burada:
- \rho: İzolasyon malzemesinin özgül direnci (Ohm-metre)
- L: Kablonun uzunluğu (metre)
- D: Kablo dış çapı (metre)
- d: İç iletken çapı (metre)
- \ln: Doğal logaritma fonksiyonu
b) İzolasyon Malzemesinin Özgül Direncinin Hesaplanması:
Verilen bilgilere göre:
- Kablonun uzunluğu L = 2 km = 2000 m
- İletken çapı d = 5 mm = 0.005 m
- Kablo çapı D = 25 mm = 0.025 m
- İzolasyon direnci 20,000 \Omega/km = 20,000 \Omega/1,000 m = 20 \Omega/m
Özgül direnç (\rho) yukarıdaki formülden elde edilebilir. Verilen değerleri yerine koyarak:
20 = \frac{\rho}{2 \pi \times 2000} \ln\left(\frac{0.025}{0.005}\right)
Doğal logaritmayı hesaplayınız:
\ln\left(\frac{0.025}{0.005}\right) = \ln(5) \approx 1.60944
Denklemi düzenleyip \rho'yu çözebiliriz:
20 = \frac{\rho}{2 \pi \times 2000} \times 1.60944
\rho = 20 \times 2 \pi \times 2000 \div 1.60944
Bu noktada, \rho'yu hesaplamanız gerekir:
\rho \approx 100018.34 \, \Omega \cdot m
Sonuç
- Kablonun izolasyon direncinin hesaplanmasında kullanılan formül ve verilen değerlerle, izolasyon malzemesinin özgül direnci yaklaşık olarak 100018.34 \, \Omega \cdot m olarak bulunur. Bu değer, kablonun elektiksel performansının değerlendirilmesinde kullanılır.